наиболее важной характеристики обычно рассматривают дисперсионную характеристику, представляющую собой зависимость коэффициента замедления / от длины волны Я в свободном пространстве. При работе ЗС на одном и том же типе волны дисперсионная характеристика существует в пределах полосы пропускания, т. е. в пределах изменения фазового угла О Фо I я I. Этому диапазону соответствуют длины волн, лежащие между и Я|л1, для которых фазовые сдвиги основной гармоники равны либо нулю, либо ±я. В соответствии с (4.8)-(4.10)

/ = фД/(2я1е), (4.21)

и, следовательно, дисперсионные характеристики гармоник должны лежать между прямыми, выходящими из начала координат: для основных гармоник между

/о = 0, (фо = 0) и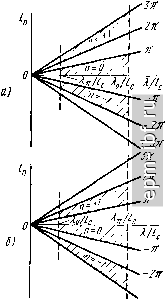

Рис. 4.3. Возможные области существования дисперсионных характеристик основной и±1-х гармоник (заштрихованы):

а - основная гармоника прямая: б основная гармоника обратная

где знак плюс соответствует прямой, а минус - обратной гармонике.

Для гармоник с I /г I = 1 при прямой основной гармонике между

-Ц' (Ф±1 = ±2я); ln=- - Q,

(ф 1 = -я) и

(ф+1 = 3л).

При обратной основной гармонике

ln=±Q, (Ф±1 = ±2Л), 1п = {,

(Ф+1 = я) и = -1. {ф-1 = -Зл).

На рис. 4.3 показаны возможные области существования дисперсионных характеристик основной и ±1-х гармоник.

Положительными принимают групповую скорость и соответствующий ей коэффициент замедления /р = c/Upp. В соответствии с (4.12)

(4.22)

hт> - n - f -п--h -

Ж

Таким образом, касательные к дисперсионным характеристикам пространственных гармоник в точках, соответствующих одному и тому же значению Я, лежащему внутри полосы пропускания, сходятся в одну точку на оси ординат, отсекая отрезок lp. На границах полосы пропускания при Я = и Я = А, , Urp = 0. а /гр = ОО- Отметим также, что внутри полосы пропускания фазовая скорость и, следова-

тельно, коэффициент замедления монотонно.

In должны изменяться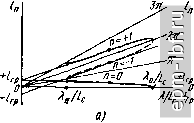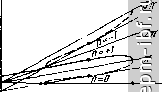

Рис. 4.4. Дисперсионные характеристики ЗС с основной прямой гармоникой (а) и основной обратной гармоникой (б)

Дисперсионные характеристики для ЗС представлены на рис. 4.4, причем характеристики обратных гармоник (пунктирные кривые) перенесены из IV в I квадрант системы координат, а групповая скорость для иих условно рассматривается как отрицательная.

Производная ветвей дисперсионной характеристики, соответствующих обратным гармоникам, всегда положительна и не может быть равна нулю, как у прямых гармоник. Это означает, что фазовая скорость обратных гармоник сильно зависит от частоты, тогда как фазовая скорость прямых в полосе рабочих частот может оставаться почти постоянной.

Второй основной параметр ЗС служит для оценки эффективности взаимодействия электронного потока с электри-

ческим полем той или иной пространственной гармоники. Очевидно, что эффективность взаимодействия tern выше, чем больше разность потенциалов, создаваемая тормозящим полем данной гармоники на единице Электрической длины системы:

.л/ря = Е, К/{2л) = АСпК/{2п).

Эффективность взаимодействия больше, если та .же напряженность тормозящего поля создается при прохождении через ЗС СВЧ электромагнитной волны меньшей мощности. Поэтому количественно эффективность взаимодействия оценивают сопротивлением связи

Рис. 4.5. Частотная зависимость потерь в ЗС

Рзе = £./(2ряР),

где Р - мощность суммарного электромагнитного процесса, передаваемая по ЗС совокупностью бесконечного числа пространственных гармоник. Коэффициент 2 в знаменателе соответствует переходу от

подставляемой в формулу амплитуды напряженности поля Egn к ее эффективному значению.

Значение сопротивления связи меняется - убывает в направлении оси у в соответствии с (4.18). Обычно рзс определяют в плоскости у = const (при отсутствии вариаций поля вдоль координаты х), где пропускают электронный поток. У различных ЗС сопротивление связи может иметь значения от нескольких десятков до нескольких сотен омов.

Наибольшее значение сопротивление связи имеет для основной гармоники. С ростом номера гармоники оно падает не только из-за уменьшения амплитуды продольного электрического поля соответствующей гармоники, но и из-за роста коэффициента фазы р„.

Сопротивление связи зависит от длины волны, поэтому его значения обычно относят к соответствующим точкам дисперсионной характеристики. Зависимость рз,. = / (Я) также является характеристикой ЗС.

СВЧ-токи, протекающие в поверхностном слое металлических проводников ЗС, вызывают потери энергии, которые