Поскольку в поперечном поле векторное произведение Iv, В] имеет максимальное значение, то и магнитная сила максимальна. Под ее действием электрон начинает двигаться по окружности, радиус R которой определяется из условия: в каждый момент времени магнитная сила F уравновешивается центробежной силой Рц. Приравнивая F и /ц, получаем evB = tnv/R, откуда

R = mv/(eB). (2.12)

Угловая скорость движения электрона по окружности (циклотронная частота)

(л^ = еВ1т. (2.13)

Как видно из выражения (2.13), Мц, а следовательно, и период вращения, не зависят от скорости электрона и определяются только магнитной ин-

дукцией В. %

Приведенные соотношения +/-

поясняют движение электронов фг /V

в электровакуумных приборах с поперечным магнитным полем, которые называются п р и б о-

р а м и М Т и п а. Рис.2.2. Движение электрона

В. Пусть скорость электрона магнитостатическом поле, V имеет произвольное направ- когда угол между v и В ление по отношению к магнит- равен 90°

ной индукции В. Траектория

электрона в этом случае будет спиральной, причем радиус спирали определяется поперечной составляющей скорости, а ее шаг - продольной составляющей.

3. Движение электрона в сложных статических полях

Рассмотрим случай, когда в пространстве, где движется электрон, действуют одновременно как электрическое, так и магнитное статические поля.

Уравнение движения электрона в этом случае имеет вид

F = ma = F,-f F = -e(E-f[v, В]), (2.14)

где а - ускорение электрона.

Решение уравнения (2.14) рассмотрим для частных случаев, имеющих определенный практический интерес. Движение электрона представим в прямоугольной системе координат.

А. Предположим, что = By = 0; В^ = В; Еу = = Ег = 0; Ех = -Е, т. е. имеем случай скрещенных полей [Е L В). Записывая (2.14) по осям прямоугольной системы координат, получаем

m = -e{-E+iB

Решая последние уравнения относительно х ц у для начальных условий: / = О, л; = О, у = О, dyldt = О, получаем

л; = 0(1-cosMO; (2-15)

у = о(Шц-8ШШц0, (2.16)

где

D = m£/(eB2)==£/(to5).

Выражения (2.15) и (2.16) являются уравнениями циклоиды**, т. е. электрон движется по циклоидальной траектории.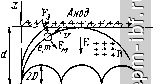

Рис. 2.3. Движение электрона в скрещенных статических полях, когда Вг = В и Ех = -£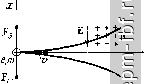

Катод

Рис. 2.4. Движение электрона в скрещенных статических полях, когда его начальная скорость Vy=-V

Траектории движения электрона для случая скрещенных полей в плоском диоде представлены на рис. 2.3. В зависимости от соотношения между напряженностью электрического поля Е и магнитной индукцией В электрон, покидая катод, или вновь на него возвращается, не достигнув анода,

* Циклоида - это кривая, описываемая точкой круга [в данном случае с радиусом R (2.12)], катящегося по плоскости. Если круг катится по цилиндрической поверхности, то описывается эпициклоида.

или же попадает на анод. Граничным следует считать тот случай, когда траектория касательна к плоскости анода 2D = d. При этом значение магнитной индукции называется критическим - В^р-

Преобразуя выражение для D, получаем

5кр = V 2mEj{ed) = Y2mUleld.

(2.17)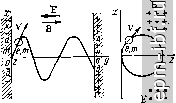

Если В > 5кр. то электрон, вылетая из катода, вновь на него возвращается. Если В < В^р, то электрон попадает на анод.

Если электрон в начальный момент времени (/ = 0) не находится в состоянии покоя, а движется в направлении оси у, то траектория его движения имеет уже другой характер (рис. 2.4). Электрон влетает в пространство взаимодействия со скоростью Vy - V. На него действуют силы Fg и F , направленные в противоположные стороны. Если I Fg > I F I, то электрон при движении приближается к аноду. В противном случае электрон отклоняется к катоду. Если F, = = 1 F 1, то электрон движется по прямой линии со скоростью

v = ElB. (2.18)

Рассмотренные примеры соответствуют движению электронов в магнетронных генераторах и лампах прямой или обратной волны М-типа.

Б. Пусть теперь Ех = Eg = 0; Еу - -Е; Вх = Вц = 0; By = В. Этот случай также рассмотрим на примере плоского диода (рис. 2.5).

Если электрон влетает в пространство взаимодействия со скоростью, которая направлена по оси г/, то он ускоряется электрическим полем и движется равноускоренно по прямолинейной траектории.

Если же скорость электрона имеет составляющие как по оси у, так и по оси х, то электрон движется по спирали со все увеличивающимся шагом. Радиус спирали опреде-

Рис. 2.5. Движение электрона в скрещенных статических полях, когда начальная скорость электрона имеет составляющие как по оси X, так и по оси у