ной. При этом внешние цепи могут быть подключены к МУ последовательно или параллельно. Так, для коаксиальных линий с внешней заземленной жилой удобнее применить параллельное подключение входов. Для полоскового или микрополоскового исполнения может оказаться предпочтительной симметричная нагрузка, которая подключается последовательно. Параллельное подключение волноводов осуш,ествляется тройником в плоскости Я, последовательное- тройником в плоскости Е (рис. 5.2).

Мостовые устройства рис. 5.1 допускают без нарушения развязки между входами следующие изменения электрических длин плеч:

а) любое из них можно изменить иа целое число воли (± пЦ;

б) два смежных плеча можно изменить на ± V2.

Если пара развязанных входов (/-2 или 3-4) подключена к МУ идентично, т. е. последовательно или параллельно, то электрические длины линий, соединяющих эти входы, должны отличаться на Я/2 (см. рис. 5.1, а, г, е); тем самым создается возможность развязки между ними. При этом, однако, развязка зависит от частоты.

Если один из развязанных входов подключен последовательно, а другой параллельно, то условием развязки является равенство длин линий, соединяющих эти входы (например, рис. 5.1, б, в W д - входы 3 - 4). Поскольку фазовые соотношения у линий с одинаковыми длинами сохраняются иа всех частотах, то развязка получается частотно-независимой.

Поворот фазы на 180°, необходимый для развязки между парой входов, может быть также осуществлен перекрещиванием проводников у двухпроводной линии (см. рис. 1.8) или скруткой волновода. При этом в МУ (рис. 5.1, е) плечо длиной ЗЯ/4 может быть заменено отрезком длиной Я/4, тогда все четыре плеча будут иметь одинаковую длину (Я/4) и развязка будет частотно-независимой.

Аналогично коэффициент деления мощности т между развязанными входами ие зависит от частоты, когда длины плеч, соединяющих эти входы со входом, к которому подключен источник, одинаковы.

Найдем данные гибридного кольца (рис. 1.9). Ему соответствует схема рис. 5.1, е. Соотношения волновых сопротивлений плеч определяются заданными величинами Zbx и т. Эффект подключения генератора ко входу / ие изменится, если закоротить развязан-

ный вход 2. Тогда согласно (2.19) 1 541 V Sg I

PJP 51 = m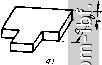

Рис. 5.2. Способы подключения к волноводному МУ:

а -тройник в плоскости ; б - тройник в плоскости е

откуда соотношение волновых сопротивлений плеч WW - = YmYRjPZ- Если = R = R, то

= У^Г ; Zbxi= Wl.WlJR {Wl, + WIJ = mWlJil + m)R,

(5.1)

При условии Zbxi = R волновые сопротивления W = = R У (I + m)/m, Wi3= R Vl + m. Подключив генератор ко входу 2, находим аналогичным образом соотношение волновых сопротивлений плеч 2-3 и 2-4. Накладывая условие Zbx2 = R, получим 124 = R 1/1 + т; Г23 = Р Ут/(1 + т) . При m = 1 волновые сопротивления Ws = = 23 24 = К2 R. В общем случае, когда РиФ Рб,

= VRn Rn (1 + rn)/m, Г13 - VRn Ro (i+m),

(5.2)

Обратимся к схеме рис. 5.1,5 с разнородной подключенно парой входов 3-4, развязанной независимо от частоты. При подключении к последовательному входу несимметричного генератора или нагрузки необходим четвертьволновый симметрирующий трансформатор. На рис. 5.3,а представлено конструктивное выполнение устройства иа коаксиальных линиях. При применении полосковых линий удобно подключать развязывающее сопротивление к последовательному входу в виде симметричиого^напылениого) резистора. При /и = 1 и

/? = Рб = имеем W = У'2 R и Zbxi = вхг =

Если в схеме рис. 5.1,5 укоротить два смежных плеча на Я/2, то получится так называемое укороченное кольцо или U-moct (рис. 1.7). Этот видМУ получил широкое распространение в микро-полосковом исполнении (рис. 5.3,6) благодаря малым габаритам и достаточно хорошим полосовым свойствам. Он является исходным для построения многополюсных МУ с поворотной симметрией. Когда МУ работает в режиме деления мощности генератора, подключенного ко входу 4, коэффициент деления т не зависит от частоты, так как 54 = 524- Развязка входов 3 и4 частотно-независима, т. е. S34 = 0. Входы 1 и 2 развязаны только иа средней частоте, когда I = Я/4.

ю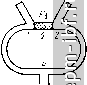

Рис. 5.3. Кольцевые МУ: коаксиальное (а); полосковое укорочеппое кольцо (б)

Волновые сопротивления плеч могут быть найдены таким же способом, как и для гибридного кольца. Развязка входов /, 2 на средней частоте выполняется при = Я^Д^1т и =

= mRRs, соответственно Wi = mWu-

2вх1 = {WUm)/[R (1 + т)] = R 1{т + 1). (5.3),

2вх2 = IAR (1 + т)] = Rmlim + 1).

При m = 1 =W2i=w = УЖЖ^ Zbxi = Zbx2 = /?б/2.

При Рн = P

= 24 = К2 /?, Re = 2P, Zbxi = Zbx2 = R- (5.4)

При использовании МУ в многополюсных системах, как будет показано ниже, можно, выбирая различные величины волновых сопротивлений в разных МУ, расширять полосы пропускания.

На рис. 5.4 приведены частотные характеристики при т = 1 гибридного кольца (/) и укороченного кольца (2). Широко распространенным является также квадратный или, как его иногда называют, шлейфный мост (рис. 1.10). Большим достоинством его является конструктивная симметрия и простота выполнения. (Отсчет длин плеч ведется от середины пересечения линий; при больших толщинах линий их электрическая длина несколько укорачивается из-за неоднородности в месте стыков.)

Квадратный мост относится к классу квадратурных. У него развязаны две пары соседних входов (1-2 и 3-4 на рис. 5.5). Развязка между ними на средней частоте (/ = V4) выполняется при условии wa wc Рнб = WaWoiWh + Р„Рб). При этом входные сопротивления

Zbxi = Rh (Wawd/wcwb), Zbx2 = Ro (wawb/wcwd).

Если выполнить этот МУ симметричным, т. е. положить wb = wd

и Wc= Wa, а также Р„ =

Рб = Р, то условие развязки будет: rw\ = Wh {W% + r%

Из приведенных соотношений

и заданных т необходимые величины вых сопротивлений плеч.

можно найти волно-

Пусть

1,0 v - 7,zm

Рис. 5.4. Частотные характеристики гибридного (/) и укороченного (2) кольцевых МУ

Рис. 5.5. Простой квадратный мост 72

9 >.

2вх1 = .вхг = R, ReRnR, тогда =Р, 1Гв = = Ут/(т + i) r. При m = 1 имеем Wa = r, Гв= Р/]/ 2. У одного плеча волновое сопротивление такое же, как у входных линий, а у другого оно меньше (у большинства кольцевых МУ волновое сопротивление больше), это представляет некоторое конструктивное достоинство, так как при микрополосковом исполнении большие величины W осуществить затруднительно.

Недостатком квадратного моста является зависимость от частоты всех параметров (, т, Zbx)- Можно рекомендовать применять его при полосах пропускания не более 5-6%. На рис. 5.6 приведены частотные зависимости для моста с m = 1: развязки , КБВ и коэффициентов передачи в нагрузки S13, 8ц.

В некоторых случаях удобно иметь устройство, также построенное без изгибов плеч, но симметричное относительно нагрузки Р„. Таким является мост на сопряженных квадратах (рис. 5.7), имеющий два развязывающих сопротивления. Такой мост так же, как и укороченное кольцо, может служить основой для построения многополюсного МУ с поворотной симметрией (см. [8] ч. I). Условие развязки при равенстве волновых сопротивлений противоположных плеч

Г л = ГвК(2Рн RM2Ru Ro - W%). Входные сопротивления

Zbxi = вх2 = rq/wb-

(5.5) (5.6)

При Zbxi = 3x2 = Р„ = Рб = /? wb = R, wa = y2R.

Полосовые свойства МУ можно, как показал В. Бушбек [36], улучшить путем соответствующего подбора волновых сопротивлений wb, wa и соотношения Ре/Ри- Так, например, при Рб = 0,63 Р„, wa = 2,2\ Р„ и неодинаковых волновых сопротивлениях вертикальных плеч (среднего Wh = 1,56 Р„ и крайних Гв = 0,79 Р^) развязка 20 дБ сохраняется в полосе частот порядка 20%, т. е. при-

gff КБВ

1,S f/fa

1 1,5 f/fg

Рис 5.6. Частотные характеристики квадратного МУ Рис. 5.7. МУ иа сопряженных квадратах

близительно в 2 раза более широкой, чем при указанных выше (5.6) соотношениях. Некоторым недостатком такого исполнения МУ является различие величин сопротивлений нагрузки и балласта и значительное расхождение величин волновых сопротивлений плеч.

5.2. устройств. с расширенной полосой частот

Рассмотренные в § 5.1 простые устройства могут быть развиты с целью расширения полосы частот. Так, укороченное кольцо (одно-секционное МУ) можно дополнить до -секционного (рис. 5.8) *. При этом, как и для трансформатора сопротивлений, увеличение числа четвертьволновых ступеней позволяет расширить полосу частот или улучшить согласование за счет компенсации отражений иа стыках секций, а благодаря набору резисторов Ri, R, Rs, . . ., Rn увеличивается развязка.

Параметры такого МУ, симметричного относительно входов 2 и 3, находятся с помощью метода синфазного и противофазного возбуждений (§ 2.2). Синфазному (рабочему) режиму соответствует ступенчатый трансформатор, теория которого достаточно хорошо разработана [6-9,13] и позволяет оптимизировать модуль коэффициента отражения S+ = Граб J-

В противофазном режиме участвуют развязывающие резисторы, величины сопротивлений которых выбираются так, чтобы коэффициенты отражения S~ и S+ возможно меньше различались в рабочей полосе частот. Согласно (2.35) это обеспечивает наибольшую развязку между входами 2 и 3. Число секций, необходимое для реализации задаваемого 5+ (щах при относительной полосе пропускания

= (/шах - fmin)/(fmax + Lin) 2А /о, (5.7)

c=yj-

-I--x-i-

Рис. 5.8. Многосекционное МУ \9 ]ma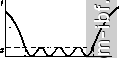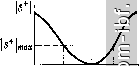

Рис. 5.9. Зависимости 5+ = [Граб

a - чебышевская; б - максимально плоская

* В [11] предложен однотипный вариант МУ на двухпроводных линиях.

составляет: для чебышевской характеристики (рис. 5.9, а)

Arch(y l-5+,Lx/2T2 S+Lnx ) Arch[l/sin(.4Af/4)] a для максимально плоской (рис. 5.9, б)

Ig [2 I S+ п,<пх/ /ГН5+й

lg[cos(n/2)(l -Д/Р/2)] что иллюстрируется рис. 5.10. При обеих упомянутых характеристиках [61 для двухсекционного МУ при R = l ttjR = 2,

Р, = 2R (Г, + W)I{R (Г, + й^) - 2 W],

гдех -линии.

Таблица 5.1

Рз = 4IVWT+ W,) (Гг- г, ctg2 X), значения х, при которых S = 0; х - электрическая длина

Для максимально плоской характеристики x=nl2. Для чебышевской характеристики нули определяются равенством cos х' = (1/К2) X X sin (лЛ FI2), а при х = я/2 S+ == Re S = {2W\ - - Wl )/(2 Wl + Wl),

S- = [(2/Рг) (1-2/Pi) -- l/rj]/[(2/P2) X X (l+2/Рг) + \IW\].

Результаты расчета рабочих параметров двух-, трех-и четырехсекциоииых МУ с чебышевской частотной характеристикой для различных значений а = /в н приведены в табл. 5.1.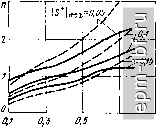

0,7 ZiF

Рис. 5.10. Определение числа секций му по ширине полосы пропускання и допуску па рассогласование