- {2r/lF2) = 0. Полагая заданным отношение iF/lFa = k, в этом случае имеем Wi = W {I + /г)/ /г и, соотвественно,

W-2.

ctgx

~ + k~~c\gx+j2W~

(ft~Mgx-ctg x)

Принимая k = I, 1/2, 1/4, 1/6 и находя величины W соответственно из условия S = О при X = 60°, 45°, 30° и 24°, получаем зависимости, приведенные на рис. 5.22, где для k = l IF = 0,6124, для k=-.l/2 1Г = 0,378,для й= 1/4 Г=0,218, для й = 1/6 7=0,1526.

Глава 6

МОСТОВЫЕ УСТРОЙСТВА НА СВЯЗАННЫХ ЛИНИЯХ

6.1. простейшие .му

Простейшее МУ на связанных линиях (рис. 6.1) является квадратурным и часто называется направленным ответвителем (НО)*. НО получили широкое распространение вследствие их широкополос-ности, принципиально полной развязки, согласования независимо от частоты и простоты конструкции [14, 15, 31]. Они могут выполняться на различных типах линий передачи: двухпроводных [18, 24], полосковых и волноводах.

Устройство обладает полной симметрией (см. § 2.2), поэтому частотные зависимости его коэффициента деления т могут быть определены методом синфазно-противофазного возбуждения. В синфазном режиме обе линии НО эквипотенциальны и устройство можно разделить на два несвязанных отрезка линий передачи с волновым сопротивлением W+, нагруженных на концах на номинальные сопротивления R. В противофазном режиме напряжения на линиях НО противофазны и устройство можно разделить на два несвязанных отрезка линий с волновым сопротивлением W~, также нагруженных на R.

Параметры рассеяния для синфазного и противофазного возбуждений:

3 г

Рис. 6.1. Направленный ответ-витель в режиме деления мои^-ности

= 5з± =(?-r±)ctgx/[(r± + +?)ctgл;+2/l/pr±], (6.1) S± = -2RY\-Yzitxl{{R-Y + r±)ctgx + 2 pr±], (6.2)

* Такое название отвечает принципу направленной передачи мощности из одной линии в другую.

где верхний знак соответствует синфазному режиму, а нижний - противофазному; х = 2 я я = я 2/о.

Вследствие полного согласования S = = 0. С учетом этого и соотношений (6.1), (6.2) условие согласования и развязки принимает вид R = YW+W-. Используя свойства симметрии и формулы (6.1), (6.2), определим значаш,ие элементы матрицы (2.25) - коэффициенты передачи

р = = 2 R/[2R COSX + i{W+ - W-) sinx], (6.3)

y = jYl-~Pe-i<f = {W+~W) sin x/[2R COSX+ + fiW+ - W-) sinx],

(6.4)

где t = l/Y (tn + 1) - m cosx; ф = arctg[(m + 1) tg x]. При

этом I Ymax I = Ymlim + 1); Pmax = 1/Kl + m. Величины W+ и W~ находятся из соотношения

r+/P=P/r-= {Y\T + YmYl{YU~VmY\ (6.5)

кроме коэффициента деления по мощности, НО часто характеризуется переходным ослаблением в децибелах

С41 = 10 lg/S4i I = 10 Ig (1 + т)1т;

при m = 1 С41 = 3,01 дБ.

Равноплечий НО (т = 1) обеспечивает весьма широкую полосу пропускания (рис. 6.2). Так, при неравномерности коэффициента деления + 10% относительная полоса пропускания составляет 0,6 (коэффициент перекрытия по частоте а = 1,85). При увеличении т полоса сужается.

Для работы в широкой полосе частот в [3] рекомендуется применять мосты с m > I, так как при одном и том же допуске на изме-. . некие коэффициента деления в по-

лосе частот получаем более широ-

кую полосу (рис. 6.3). Задаваясь

0,8 0,1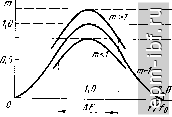

о 0, 0,8 7,2 7,6 f/fo

Рис. 6.2. Зависимость коэффициентов передачи по мощности но при согласованных нагрузках

Рис. 6.3. Частотная зависимость коэффициента деления но по мощности при различных номинальных значениях гч

допуском на коэффициент деления Am и величину а, нетрудно определить

л-apcsin ml(m -f Am)

или

F=2 \

arcsinm/(m4-Am) 2

arcsin

m -j- Am

Результаты расчетов a, a также нормированных значений W+IR и для различных Am приведены в табл. 6.1. В режиме деления мощности (рис. 6.1) НО возбуждается со входа 7, а к остальным выходам подключаются нагрузки. При рассогласовании нагрузок их коэффициенты отражения равны соответственно Га, Гз, г4, нормированные волны определяются по следующим формулам:

&4 =

/2 Гз-(1-2)г,-Г4 Гз Г2e-Ф 1-/2 Га Г. е-2/ч)4-(1-2)Гз Г^е-

ИУ1{Т, + Т,)

\-РТ, Г, е- З'Ф+С! -/2) Гз Г, е- (1-Г2Г4)е-2ч'

1-2 Г2Г4е-2ч'-1-(1-/2) Гз Гге-З'Ф

/Т^Ь=(1+Гз Г,е-2Ф) \~~tr,r е-2*Н-(1-/ )ГзГ2е-2/

е- 2/ч> а^, е-2/Фа

е-2/Фс1, e-2/<Pai.

(6.6)

Из рис. 6.4, построенного в соответствии с (6.6), видно, что при одинаковых рассогласованных нагрузках и согласованной балластной нагрузке, имеющей место в большинстве практических случаев, входной коэффициент отражения делителя значительно меньше коэффициента отражения нагрузок. Это свойство выравнивания входного коэффициента отражения, отмеченное в [18], позволяет значительно улучшить согласование нагрузок с источником сигнала.

Полосковые МУ на связанных линиях могут исполняться по-разному, в зависимости от величины т. При малых значениях т (слабой связи) широкое распространение получили симметричные и несимметричные НО с боковой связью (рис. 6.5, а и б). Расчеты таких НО изложены в [6, 7].

С приближением m к единице зазор между полосковыми проводниками становится очень малым, что приводит к технологическим трудностям при изготовлении. Кроме этого, в несимметричных НО синфазная составляющая распространяется в основном в воздухе, в то время как противофазная сосредоточена в диэлектрике. Вследствие различия диэлектрической проницаемости воздуха и диэлектрика возникает разность скоростей распространения этих видов колебаний, возрастающая с увеличением связи. Это приводит к ухудшению направленности и согласования. 84

В равноплечем полосковом НО чаще всего используется лицевая связь (рис. 6.5, в). Конструкция симметрична, поэтому лишена недостатков, присущих несимметричному НО с лицевой связью. Методика расчета НО с лицевой связью изложена в [9, 14]. Глубокую связь (т > 1) можно обеспечить в связанных линиях с дополнительной изолированной проводящей пластиной связи как в симметричном, так и в несимметричном исполнении (рис. 6.5, г, д). При этом лицевая связь между полосковыми проводниками может практически отсутствовать. Расчет таких НО удобно проводить, используя свойство симметрии. Внешнюю (пластина связи -земля) и внутреннюю (полосковые проводники -пластина связи) системы можно считать независимыми, если с > (2й + 6 + 4/I2).

Найдем волновые сопротивления для схем синфазного и противофазного возбуждений:

- для симметричной конструкции (рис. 6.5, г)

W+ = W,+ Wz, W- = W2, (6.7)

- для несимметричной конструкции (рис. 6.5, д).

W + = 2Wi + W2; W-= W2, (6.8)

где Wi - волновое сопротивление пластины связи относительно земли; W, - волновое сопротивление полоскового проводника

Таблица 6.1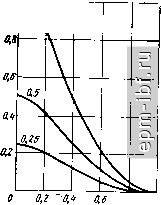

0,8 f/fg

Рис. 6.4. Частотная зависимость входного коэффициента отражения НО при одинаково рассогласоваипых нагрузках

Рис. 6.5. Поперечные разрезы НО:

а-полосковыП симметричный с боковой связью; б-то же несимметриче.ыП; в - полос-ковый симметричный с лицспоП спязью; г - полосковын симмстричкыи с дополнительной пластинкой связи; д - то же несимметричный

относительно пластин связи. Выбор величин W+ и W~ производится по заданному т из соотношения (6.5). Геометрические размеры проводников находятся раздельно для внешней и внутренней частей на основании (6.7) и (6.8) соответственно по известным соотношениям для симметричных или несимметричных одиночных полосковых линий [6].

Связь между линиями в НО может быть осуш,ествлена с помош,ью сосредоточенных емкостей [19, 20]. При этом можно получить сокращение габаритов устройства, что важно в метровом и дециметровом диапазонах. Устройство отличается простотой конструкции (рис.6.6, а) и может выполняться на отрезках коаксиальных или полосковых линий передачи. Схема НО симметрична относительно горизонтальной и вертикальной осей, эквивалентная схема при синфазном возбуждении представляет собой отрезок линии с волновым сопротивлением R и согласованными нагрузками на концах (рис. 6.6, б). Значащие элементы матрицы рассеяния синфазного режима возбуждения соответственно равны

S+ = cos X - / sin X. (6.9)

Эквивалентная схема противофазного возбуждения представляет собой отрезок линии с тем же волновым сопротивлением R, нагруженный на концах сопротивлениями R и емкостями 2 С (рис. б.б, в). Элементы матрицы рассеяния имеют вид

[l + (2(oCJ?-ctgx)]sinx-l 11 33 [i i /(2(oC/?-ctga:)]2sin2a:-f Г

2/sin;. (6-10)

[I+/(2(oC/?-ctgx)]2 sin= л: + 1

Так как S+ = О, то из условия согласования на центральной частоте следует, что S- = О и

соС/? = ctgx . (6.11)

Из соотношений (6.9), (6.10) с учетом (6.11) найдем параметры рассеяния, характеризующие передачи

5Гз =

xctgXmjl - x ctgХт cos х) +ix ctg2 Xm sin X

2x ctg Xm cos X- 2x2 ctg2 x,n sin x + sinx + j {2x ctg sin л: -cos x)

(6.12)

о ctg Xm-x ctg Xm sin X cos x +jx ctg2 Xm sin X-j

-13----

2x ctg Xm cos x-2x ctg2 Xm sin x + sin дс+/ (2x ctg Xm sin x - cos x)

-*- о- 3 - - -C I JIM-1 I o- -

WP 5 R

Рис. 6.6. Схема полоскового НО с емкостной связью (а), его эквивалентные

схемы при синфазном (б) и противофазном (в) возбуждении

На центральной частоте диапазона х = х^ Из (6.12) следует

I Si4 Р = COS Хт, Si3 I = Sin Xm, ГП = ctgX. (6.13)

НО с емкостной связью является сонаправленным. В равноплечем НО Хт = л;/4, следовательно, длина линий составляет Я/8, что вдвое короче длины линий НО с электромагнитной связью. С уменьшением коэффициента деления по мощности длина линий НО увеличивается, стремясь к Я/4. Полоса пропускания НО с емкостной связью меньше, чем у НО с электромагнитной связью, и составляет 0,1 для т = 1 при неравномерности по мощности 10%. В этой же полосе развязка не менее 20 дБ (рис. 6.7).

6.2. МНОГОСЕКЦИОННЫЕ НО

Существенное расширение полосы по коэффициенту деления в сравнении с односекционными НО при сохранении идеального согласования и развязки достигается в многосекционных НО, которые могут быть симметричными и асимметричными. Симметричные НО (секции, равноотстоящие от середины, одинаковы) являются квадратурными, поэтому данный тип МУ представляет больший практический интерес (рис. 6.8).

Для синтеза симметричного НО, имеющего оптимальные с точки зрения функции передачи характеристики в широкой полосе частот, используются полиномы Чебышева [8,13]. Значительное упрощение расчета дает сведение многосекционного НО к многоступенчатому эквивалентному трансформатору сопротивлений [21, 23].

Рассмотрим ступенчатый трансформатор (рис. 6.9) с секциями равной электрической длины х. Крайние секции одинаковы и имеют волновое сопротивление W, а средняя - сопротивление W.

Рис. 6.7. Частотная зависимость коэффициента передачи по мощности и развязки между каналами НО с емкостной связью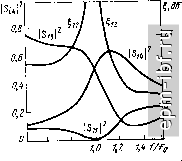

0,6 0,8

2

Of -1

- Wo IVf Wq -r

Рис. 6.8. Схема симметричного многосекцнонного НО Рис. 6.9. Эквивалентный ступенчатый трансформатор