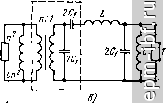
мальная работа МУ может нарушиться на верхних частотах КВ диапазона из-за индуктивностей проводников, соединяющих конденсаторы. Эти обстоятельства должны быть учтены при конструировании МУ.

Входные сопротивления моста = 2xR/{R + 4л;*) +

+ j Ix + Rx/{R + 4д:*)] = Гвх + /Хвх зависят от частоты. Поэтому питающие фидеры должны подключаться ко входам через согласующие контуры, трансформирующие Zbx в = Ц7. На рис. 9.3, б, в показаны два варианта согласующих контуров. Если R > Гвх, то используется схема рис. 9.3, б, причем Xi = ±У Гвх {R - / вх) -

- Хвх, Х2=- ±R Гвх/]/Гвх {R - Гвх)- Если R < (г|х + Л;х)/Гвх= = \/g, то используется схема рис. 9.3, в, у которой Xi =

= +VR i/g-R),

Необходимость в громоздких согласующих контурах является существенным недостатком данного МУ.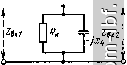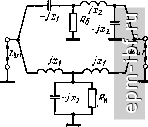

Рис. 9.1. Схема ТМ-моста

Рис. 9.2. Схема ТМ-моста с заземленной балластной нагрузкой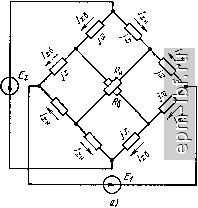

I Х

\R 4

Рис. 9.3. Двойной мост:

а - схема, б и в - варианты согласования на входах 130

9.2. СИНФАЗНО-ПРОТИВОФАЗНЫЕ УСТРОЙСТВА С полной РАЗВЯЗКОР1

Заменив на рис. 1.8 каждый отрезок линии П-фильтром нижних частот, получим схему (рис. 9.4, а), в которой имеется полная частотно-независимая развязка между входами /-2 и 3-4. Если принять 2Ci = С, а 1 = то коэффициент отражения на любом из входов один и тот же и определится в этом случае цепью (рис. 9.4, б), полученной при закорачивании развязанного входа. Эта исходная цепь для формирования всего устройства есть простой квазиполиномиальный полосно-пропускающий фильтр (см. ч. I, [19]) с дополнительным условием - равенством величин индуктивностей Г-звена (или коэффициентом трансформации, равным двум). Это условие ограничивает перекрытие по частоте а = = /в н м определяет функцию S max = / ( )*. зависящую от вида характеристики S = / ((о). Обычно предпочтительна чебышевская характеристика, для которой нормированные (к = 1) величины элементов схемы рис. 9.4, б составляют (см. ч. I, [16], приложение)

С = 4ео Ка/(а - 1)*, L = (а - 1)*/2 К2ео (а + 1),

где 8о - единственный положительный корень уравнения

16а

(а-1)4 L (а-1)* 2

(а+1)2 (а-1)

-8* 8а

. (а-1)* (а2-1)2

(а + 1)

= 0,

существующий только, когда коэффициент при е* положителен.

Соответствующая величина ISImax. зависящая от а (кривая / на рис. 9.5), связана с упомянутым корнем уравнения соотношением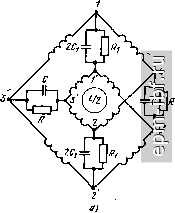

Рис. 9.4. Схема МУ с частотно-независимой развязкой, имеющая все индуктивности, равные i/2 (а), и формирующая цепь (б)

О

* I S 1 max - наибольшее значение S на рабочем интервале [co , в]. 5* 131

5max = бо/К 1 + e. Для снижения 5 ах (или увеличения а) можно ввести корректирующие элементы, в частности идентичные Г-звенья LftCй-фильтpa нижних частот между нагрузками и конденсаторами С на двух взаимно развязанных входах Зя 4 (рис. 9.6, а). Ввиду симметричного расположения шунтирующей индуктивности L в цепи (рис. 9.6, б) примем, что 2/?i = R = \ (нормирование), Lft = L, Си = Ci и найдем S \ = / (а) на входах 1 и 2.

Расчет величин элементов этой схемы для чебышевской характеристики модуля коэффициента отражения основан на использовании известного (см. ч. I, [19]) аналитического решения для функции рабочего коэффициента передачи 5 (/Q) f от нормированной частотной переменной q и метода синтеза симметричных цепей (см. ч. I, [16]), согласно которому составляется уравнение

5(а+1) -8а . 5(а + 1) -4а [2 (a-fl) -(a-lf ] 4 16

(а+1) (а-1)з , а(а + 1)

16е

(9.1)

где р - комплексная частотная переменная (нормированная); на мнимой оси р = jq. При задаваемом а (если оно реализуемо) подбирается 8 = бо, т. е. 151 max, при котором выполняется равенство (1/ео)(а - if/а (а -f 1) = 4 а /(а? + Iгде а и - соответственно вещественная и мнимая части единственного корня уравнения (9.1), расположенного в левой з-полуплоскости. Это ограничение, отражающее идентичность величин трех индуктивностей схемы рис. 9.6, б, определяет зависимость (кривая 2 на рис. 9.5). Далее, по

известным а, е^, и находятся нормированные величины элементов: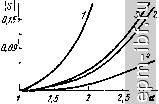

Ci = V2laol. = ;

0,S3-

2еоа(а-Ь1) q 32ео (а§+6о1 ) (а-1)3(а+1)

Рис. 9.5. Зависимости Smax=f(a) для МУ на основе рис. 9.4

(к/г

1;г

Рис. 9.6. Корректирующее звено для МУ (а), формирующая цепь (б) J32

Так, в частности, при а = 2 и соответствующем 8о = 0,0583 нормированные величины элементов схемы рис. 9.6, б составят: С^ 0,6848, L 0,475, С^ 1,953.

Другая простая коррекция состоит в подключении идентичных Г-звеньев фильтров верхних частот (рис. 9.7, а) на любых двух BsanMj но развязанных входах. Примем, что в этом случае формирующий полосно-пропускающий фильтр (рис. 9.7, б) получен в результате реактансного преобразования вещественной частотной переменной (см. ч. I, [19])

Q = (0)2 - (о^ )/(о, (9.2)

примененного к прототипу - симметричному П-фильтру нижних частот. Определим соответствующую зависимость ( 5 ( max = /(о')-Индуктивность L параллельного контура L - С, настроенного на частоту ©о = / (о„сйв, равна индуктивности продольной ветви, определяемой прототипом и составляющей L = L /(cOb-(о„).

Таким образом, элементы L и С должны удовлетворять соотношению 1/УТС = >со сов = (сОв - co )/1-LiiCh или

(9.3) и Ов =

= (сс - 1)/ KL Ch,

где L и Сн - нормированные (относительно ? = I Ом = 1 рад/с) элементы прототипа. Из (9.3) находим, что

а = 1 + (ChLh/2) + vcuul + C Lh/4) . Для чебышевской характеристики

3

-3 Л

V

(9.4)

i+ Ki-lsiLx

l-rV 1-S

I SI,

l-l-l

max-

(9.5)

I S Imax

Используя (9.4) и (9.5), находим зависимость (кривая 3 на рис.9.5)

Рис. 9.7. Корректирующее звеио МУ (о), формирующая цепь (б) для расчета коэффициента отражения на входах 3 ч 4 и эквивалентная ей схема (в) ... - .Xsilt..

Для максимально плоской характеристики C L = 2. При этом 5 = О на частоте со, = ]/ш„й)в. а подставив C L = 2 в (9.4) находим, что а = 2 + уз. Теперь осталось определить величины элементов R, L, Си С^. Из эквивалентности схем, обведенных штриховой линией на рис. 9.7, б, в, видно, что

C=C, = 2Q, п = 2, 1, L, = 2L.

Для увеличения а можно ввести на каждый из двух взаимно раз-вязаннь1х входов вместо Г-звена более сложную корректирующую цепь. Однако присутствие Г-звена равных индуктивностей на одном из концов формирующей цепи обусловливает предельную зависимость mm ISI = / (а), при которой

min 5 = const < 1 на интервале [ ; ©J,

S = 1 вне интервала [ ; ©в]. (9.6)

Индуктивность L. шунтирующая нагрузку R, ограничена интегральным соотношением [92]:

в

- d(x) -

Учитывая (9.6),

имеем--

1п (1/min \S\) = nLlR или

In (1/min ( S I) = {nllR) X (o (Sb/((Ob - сОн).

(9.7)

С другой стороны, индуктивность L в продольной ветви ограничивает абсолютную ширину рабочей полосы частот в соответствии с соотношением Боде [93]:

в

d(u = nR/L.

Принимая те же условия (9.6), находим, что

1п (1/min I SI) = nR/ ((йз - (o )L. (9.8)

Уравнивая левые и правые части выражений (9.7) и (9.8), получаем

/(ОнШв = R/L. Подставив это значение R/L в (9.7), будем иметь окончательно

min ISI = ехр [-я ]/ а/(а - 1)], (9.9)

что иллюстрируется кривой 4 на рис. 9.5.

Соотношение (9.9), не допускающее лишь а = оо, выводится и конструктивным путем, указывающим принцип схемного построения. Учитывая соотношение (9.8), примем, что формирующая цепь строится на основе преобразования (9.2), примененного к прототипу - полиномиальному фильтру ниж1шх частот. В этом случае ем-134

кость в продольной ветви полосно-пропускающего фильтра, определяемая какС= 1/cOb<j)hL = [((йв--(Он) 1п (1/min ) S ))]/(0в(1)нЯ:?, равна емкости, шунтирующей сопротивление R и выражаемой, в свою очередь, соотношением С = я/[((Ов-©н)/? 1п (1/min S )], однотипным с (9.8). Приравнивая выражения для емкостей С, получим (9.9). Таким образом, эффективным средством расширения полосы является построение цепи коррекции на основе преобразования (9.2), примененного к фильтру нижних частот.

Ограничение на величину S , обусловленное соотношением (9.9), можно ослабить, если допустить корректирующие элементы на всех четырех входах. В этом случае Г-звено ограничивающих индуктивностей оказывается не на конце формирующей схемы, а в ее средней части. Поэтому зависимость min \S\ = f(a) становится более пологой, чем кривая 4 на рис. 9.5.

В общем случае по допустимому S тах и другим требованиям, в частности фильтрации, выбирается формирующая схема, определяющая общий вид функции G (/Q). При умеренных требованиях к фильтрации целесообразно ограничиться квазиполиномиальными фильтрами с функцией фильтрации вида

(9.10)

обеспечивающей наибольшую селективность фильтров с одной полосой пропускания [94, 95]. Здесь А - вещественное число, которое для определенности можно считать положительным и таким, что 1 ()гаах = 1 на интервале [q ; qb]; oi - нормированная частота нулевого затухания; v - натуральное число.

Для квазиполиномиальных фильтров, описываемых функцией (9.10), существует простая связь величин п и v со структурой цепи (см. ч. I, [16]). Определив по выбранной структуре величины п й v, можно на основе известных методов наилучшего приближения (см. ч. I, [19], [94]) решить аппроксимационную задачу, т. е. найти численные значения величин qq г - Затем, в соответствии с общей методикой реализации (ч. I, [19]), составляется функция рабочего коэффициента передачи

G (Й*) = [1 + е*Я (Q)]-i = 1 - I S (jQ) Л

(9.11)

но в отличие от прямого решения далее требуется итерационный процесс подбора величины е = е^, при которой удовлетворяется ограничивающее условие - равенство индуктивностей Г-звена.

Это ограничение можно существенно ослабить и тем самым расширить полосу частот, что в простейшем случае и достигается в схеме рис'9.8, а. Шунтирующая индуктивность каждого формирующего фильтра (рис. 9.8, б) равна сумме всех его индуктивностей в'продоль-ных^ветвях. Это условие сохраняется при наращивании (числа звеньев, что позволяет обеспечить малое 5 щах при большом'а. При численном расчете также требуется итерационный процесс,