 |
 |
 |
 |
|
Главная Устройства сложения и распределения 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [ 23 ] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 чтобы обеспечить упомянутое условие для индуктивностей. Оно выражается определенным соотношением, благодаря чему каждый шаг итерации можно не доводить до определения величин элементов. Для вывода этого соотношения примем, что формирующая цепь представляет собой квазиполиномиальный фильтр с единственной шунтирующей индуктивностью, характеризуемый функцией рабочего коэффициента передачи (9.11), причем в функции (9.10) v = 1. В соответствии с типовой процедурой реализации (см. ч. I, [19]) переходим в (9.11) к комплексной частотной переменной р, т.е. G (-р^) = [1 + г^Р (р)Р {-p)V =1-5 (p)S i-p). (9.12) Применительно к функции фильтрации вида (9.10) с v = 1 можно путем простых преобразований составить общее выражение S(p) = . П(р +й§,) I где знаменатель есть полином Гурвица, образованный из корней уравнения (-р^) = О, расположенных в левой /?-полу плоскости. Теперь образуем выражение для входного сопротивления цепи со стороны единичной (нормированной) нагрузки: Z (р) =-а, -1р2 -1 + ...4 р- 2р2 + ...+а1р + 2Пй§/ I Полагая р = /Q О, находим, что шунтирующая индуктивность, выделенная на первом шаге реализации (рис. 9.9, а), равная сумме всех индуктивностей продольных ветвей, составит (9.14)  1У\ г 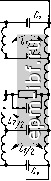 Рис. 9.8. Схема МУ с расширенной полосой (а) и формирующая цепь (б) 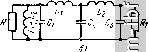 Предположим, что ту же функцию z (р) мы реализовали в симметричной схеме с равными единичными нагрузками и шунтирующей индуктивностью Lq, расположенной по Оси симметрии (рис .9.9, б). При 5 = /Q О остаются лишь эти нагрузки и шунтирующая индуктивность Lq. с одной стороны, такая цепь описывается функцией G(/Q)q-o = (2QLo) \ а с другой, при 5 = /Q О из выражения (9.11), инвариантного к коэффициенту трансформации, полу- п чаем G (/Q) Qo = еЛ nQg,7Q. Приравнивая полученные выра- п жения, находим, что Lq = 1/28Л ii Qq,-. По найденным Lqi = Ls и Lq нетрудно определить, что при коэффициенте трансформации в схеме рис. 9.9, а, равном двум, гоАаг = 2. (9.15) С учетом этого ограничиваюдего условия сформулируем этапы синтеза формирующей схемы. 1. По требуемой селективности и ориентировочно по задаваемым а и i 5 I max выбирается степень функции фильтрации п. 2. В соответствии с наиболее подходящим критерием приближения к идеальной характеристике (например, чебышевским или максимально плоским) находится функция вида (9.10). 3. По заданному 5 Imax из выражения smax = q/VI + e находится бц, подставляется в (9.12), а затем решается уравнение G-1 (-р2) = 0*. 4. По корням этого уравнения определяется коэффициент полинома Гурвица, после чего находится величина боЛа. 5. Если г^Аа-х > 2, то можно принять 5 max меньше допустимого (или большее значение а) и повторить п. 3 и 4 до выполнения равенства (9.15); может оказаться возможным понизить степень функции F (р). Если оставить избыточность в решении, т.е. г^Аох > 2, то для получения равенства Ls = Lqj следует на первом шаге реализации функции (9.13) выделить шунтирующую индуктивность, большую чем Lqi из (9.14), т. е. реализовать часть полюса функции l/z{p) при р = 0. Оставшуюся его часть можно реализовать шунтирующей индуктивностью на другом конце цепи. 6. Если egAui < 2, то следует увеличить степень функции фильтрации и далее решать задачу согласно п. 2-5. 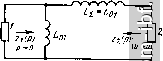 Рис. 9.9. Синтезируемая цепь (а) и симметричная цепь (б), реализующая ту же функцию G(Q2) * Поскольку F (р) вида (9.10) при v = 1 является нечетной функцией, достаточно решить уравнение 1 -f RqF (р) =0 или 1 - s-qF (р) =0, степень каждого из которых вдвое меньшая. Схемы типа рис. 9.4, а и 9.8, а в различной степени пригодны для перехода к несимметричным относительно земли входам. В схемах на основе рис. 9.4, а три плеча легко переводятся в несимметричные относительно земли. Фазоинверсное плечо должно содержать трансформатор 1:-1, недостающие элементы схемы замещения которого могут быть введены в остальные три плеча для получения попарной развязки. Естественно, что, не изменяя самого устройства, можно подключить ко входам симметрирующие трансформаторы. Только такой более сложный путь пригоден для схем типа рис. 9.8, а. Общим для обоих типов схем является возможность расширения рабочей полосы частот за счет введения связи между индуктивностями в каждом плече. При этом для каждой их пары однополяр-ными должны быть зажимы со стороны одного входа, что удобно реализуется параллельно расположенными проводниками. Полагая, например, для формирующей схемы (рис. 9.7, б) отношение шунтирующей индуктивности (со стороны единичной нагрузки) к продольной а = (1 + k)/{l - k), где k - коэффициент связи, нетрудно получить, что для определения величины а следует в (9.4) вместо Lh принять аЬ. Аналогичный эффект достигается и для схем типа рис. 9.8. Рассматриваемые устройства можно соединять согласно, например, рис. 1.14. В этом случае с целью минимизации коэффициента отражения целесообразно синтезировать формирующий фильтр для системы в целом. Если, например, в системе рис. 1.14 использовать в качестве составляющих идентичные простейшие схемы типа рис. 9.8, а, содержащие каждая лишь реактивные элементы 2Сз и L2/2, соединенные между собой симметрично через емкости С, то формирующая схема эквивалентна схеме рис. 9.7, в, но при другом ограничивающем условии. По аналогии с выводом выражения (9.4) и с учетом коэффициента связи k = (а - 1)/(а -f 1) между индук-тивностями L2/2 нетрудно получить, что а = 1 -f aLj::j4 + -f У aLJ0J2 + {aLCJAf, где произведение L Ch определяется, в частности, из (9.5). В заключение отметим, что если снять условие полной частотно-независимой развязки между входами, то нетрудно составить ряд схем, заменив в рассмотренных ранее устройствах на линиях четвертьволновый отрезок П-цепью LC-фильтра нижних частот с последующей оптимизацией параметров. Хорошие результаты, например, получены в [74] для многоканальных синфазных устройств. Осуществимы также попарные соединения устройств рис. 9.1, г [102] и другие, отвечающие различным функциональным свойствам (§ 2.3). 9.3. КВАДРАТУРНЫЕ УСТРОЙСТВА В § 2.2 было показано, что, объединив дуальные четырехполюсники, можно получать квадратурные МУ, которые часто называют направленными ответвителями (НО), поскольку механизм передачи колебаний в них аналогичен таковому для НО на связанных линиях. Объединение дуальных четырехполюсников может быть непосредственным, т. е. за счет связей между отдельными их элементами или с помощью дифференциальных трансформаторов (рис. 2.4). Один из вариантов объединения обычно более предпочтителен, а иногда является единственно выполнимым. Так, в сравнении с НО на связанных линиях, вариант с дифференциальными трансформаторами значительно сложнее. В простейшем НО [96], образованном совмещением дуальных схем (рис. 9.10), коэффициент связи между индуктивностями, образующими короткий отрезок линии, предполагается равным единице, а емкость между его проводниками -входящей в величину С. При простом анализе такой идеализированной схемы (рис. 9.10, а) методом синфазных и противофазных возбуждений видим, что если R = YLIC, то входы 1 и 2,а также 3 и 4 развязаны между собой и все они согласованы. Кроме того, при R = а^Ь = I/coqC коэффициент деления m = 1, а отношения мощностей при согласованном источнике мощности на входе / составляют: Pi/Pi = 1 + (coq/o)*, PiZ-Ps = 1 + (ш/соо). т. е. коэффициент деления m = PJPs = = [ 1 -f (со/соо)]/[ 1 4- (шоМ^]. В общем случае при 2LIR = а и сохранении условия R = VlIC получаем = /асо/(2 -f /соа), S = = 2/(2 -f /соа), 5п = = О, а m = {awl2f. Ступенчатое соединение двух таких НО [96, 97], осуществляемое с помощью идентичных согласованных отрезков линий (рис. 9.11), дает расширение полосы. При этом сохраняется дуальность четырехполюсников синфазного и противофазного возбуждений, а от электрической длины х соединяющих линий зависит соотношение между коэффициентом перекрытия а = С0в/ н и неравномерностью коэффициентов передачи мощности (рис. 9.12). С увеличением числа соединяемых таким образом НО полоса расширяется, но возрастает габарит устройства. Возможны и другие НО с расширенной полосой частот [98 , образованные иным каскадным соединением схем рис. 9.10, а, например НО, схема которого приведена на рис. 9.13. Полагая здесь 2LJR = а и 2LJR = Ь, можно показать, что при аЬ = 4 отношение PJP = 1 -f [2/{b - а)] (со -f l/co) т. е. имеет место геометрически симметричная характеристика относительно со = 1. Соотношение между аи b определяет коэффициент деления т. Например, при m=jHb - а = 4с учетом того, что аЬ = 4, находим b = 2 (1 + УЩ; а = 21 (Г+/2). 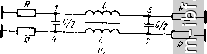 Рис. 9.10. Простейший НО: и ~ схема, б, в - составляющие дуальные цепи Можно образовать соединение и большего числа простейших НО, реализовав чебышевские характеристики коэффициентов передачи мощности в расширенной полосе частот. При этом хотя бы в одном сечении каскадно включенных составляющих НО должен быть трансформатор 1: -1 только для изменения полярности. Общим недостатком рассмотренных устройств является требование полной связи между индуктивностями (k = 1), что невыполнимо. Известны простые схемы при k 1 [99, 1001, среди которых отметим схему рис. 9.14, согласованную и полностью развязанную между входами /-4 и 2-3 лишь на средней частоте*. При k = 1 следует принять С = О и в этом случае переходим к рис. 9.10, а. С другой стороны, схема рнс. 9.14 представляет собой в сущности нулевое приближение к односекционному НО на связанных линиях (§6.1). Для лучшего приближения к характеристикам последнего можно использовать схемы на сосредоточенных постоянных, аппроксимирующие отрезок линии в достаточно широкой полосе частот [101]. Аппроксимируя короткий участок линии П-цепью фильтра нижних частот, образуем каскадное соединение п таких цепей, обеспечивающее хорошее приближение в широкой полосе частот к характеристикам линии длиной я/4. Объединив две такие схемы с помощью индуктивных и емкостных связей, получим НО (рис. 9.15), анализ которого показывает, что для равного деления мощности его характеристики уже при и = 2 мало отличаются от таковых для НО на линиях. Известны также аналогичного типа схемы на элементах с потерями [104]. В отличие от каскадного соединения однотипных П-звеньев можно использовать модифицированную двухсекционную схему (рис. 9.16) [108]. Наилучшие результаты получаются при а 0,35. В этом случае R = 1,09 V(L/C) (1 - k), QJC = А:/ (1 - k), где k = M/L. Сравнивая аппроксимируемый НО на четвертьволновом отрезке связанных линий со схемой рис. 9.16 при т = 1 (равное деление мощности; k = l/}) и отклонении направленности в пределах ±0,2 дБ, имеем отношение верхней частоты к средней у первого 1,75, а у второго 1,72. При этом рассогласование по входам мало, а развязка между входами /-4 и 2-3 велика. Если ввести магнитную связь между индуктивностями разных звеньев, то достигается а = 1,8 при высокой развязке и коэффициенте отражения на каждом входе, меньшем 5% [108]. В сравнении с рассмотренными схемами наибольшую ширину полосы имеют НО, синтезируемые по рабочим параметрам. * Аналогичные характеристики имеет НО с емкостной связью (83], удобный для работы на высоких частотах. И) Jx) (h Рис. 9.11. Функциональная схема соединения двух простейших НО 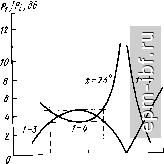 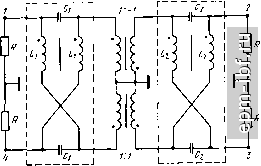 0,5 1 1,2 1,5 f/fo Рис. 9.12. Частотные характеристики H0(Pi/P3 и Я1/Я4) Рис. 9.13. Схема НО, имеющего расширенную полосу частот 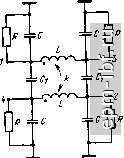 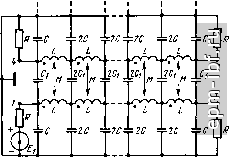 Рис. 9.14. Схема НО с неполной связью между индуктивностями Рис. 9.15. Схема, полученная в результате аппроксимации характеристик НО по рис. 1.11 Рис. 9.16. Схема двухсекционного НО с улучшенными характеристиками , И 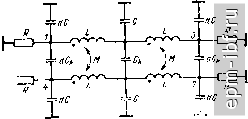 |
|
© 2007 EPM-IBF.RU
Копирование материалов разрешено в случае наличия письменного разрешения |