Если отсутствуют все фазокомпенсирующие линии, то результи-

рующая матрица [ЯЬ = 2 [Я],- или

( r)tgO-I)xo

cos-i(/-I)xo

ifi Lcos-i(/-l)A -/IF tg (/ 1) д.

(10.10)

где x - электрическая длина линии с [/ р, равным напряжению с понижающей стороны ТЛ. f ни

Используя из [25] формулы перехода к цепной матрице [А] находим ее, а затем нормированное входное сопротивление с понижающей стороны

1= I

Ь=1 =°s(i-I)xo

2 г п

L= 1 J (=1

При этом предполагаем, что нагрузка с повышающей стороны равна п, а нормированные волновые сопротивления всех линий равны W Определив коэффициент отражения как S = (z 1/п)/ (z + + l/n), нетрудно заметить, что наименьшие значения его модуля будут при Г = 1 (рис. 10.14). Для ТЛ 1 : -п при отсутствии всех фазокомпенсирующих линий матрица iHh составит

U/W)tgixo cos-i/xo L cos-ljato -jWtgiXo

(10.11)

По аналогии с предыдущим случаем находим при W = I модуль коэффициента отражения (рис. 10.14). Для ТЛ ± (1 : п), образованного согласно схеме 10.12, можно пользоваться непрерывными зависимостями на рис. 10. 14, считая, что Xq- длина линии с Up= li = и/2, и с целью сравнения брать вдвое меньшие х^.

В заключение покажем, что рассогласование можно уменьшить с помощью корректирующих сосре-

0,01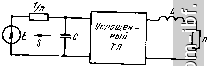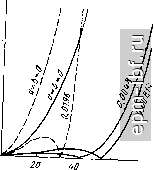

00 х,град

Рис. 10.15. ТЛ с корректирующими элементами

Рис. 10.16 Зависимости 5=/(л;) для ТЛ типа I : с корректирующими элементами (рис. 10.15); непрерывные линии для =2, штриховые - для =3 166

доточенных элементов L = axWlix> и С = bxjinW (рис. 10.15). Полагая а = Ь, что физически обусловлено асимметричностью корректируемой цепи, и используя (10.10), а также связь между матрицами [А] и [Я], нетрудно определить коэффициент отражения с понижающей стороны, который при W = 1 составит

lili - hfi- n-2/iii xa-a x

hU -hi 1 + 2-2Лц xa-a x + /2re (Лц + ax)

При различных значениях a и малых S [ах достигается существенное расширение полосы (рис. 10.16).

10.4. ТРАНСФОРМАТОРЫ С ДОПОЛНИТЕЛЬНОЙ ЛИНИЕЙ

ТЛ на раздельных магнитопроводах. Как показано в [27], при подключении к последовательно соединенным по выходам линиям дополнительной согласованной линии (рис. 10.17) можно существенно снизить продольные напряжения и благодаря этому расширить полосу частот. Физически это обусловлено введением внутренней симметрии в ТЛ.

Для изменения полярности напряжения достаточно соединить с землей другой зажим на выходе дополнительной линии.

В области нижних частот для ТЛ 1 : п при любых целых п

f/bh = 2xH- 2 U-l-

i= I

Для четных п при х = (/г/2) - 1*

fBH = fbhmln (доп) = П (П + 2)/4 - 1,

а для нечетных я и х на интервале [ (я - 1)/2; (я - 3)/2] имеем

fB =f/B mln(aon) = [(n+l)/2]-l-

Если X = (я - 1)/2, то достигается минимум суммы продольных напряжений только на основных линиях.

Для определения величин приведенных шунтирующих индуктивностей удобно воспользоваться схемой рис. 10.18, где указаны коэффициенты трансформации и продольное напряжение на дополнительной линии для четных я. Если я - четные, то коэффициент трансформации верхнего ТЛ равен (я/2) -f 1, а нижнего (я/2) - 1. Нетрудно видеть, что при четном я величина L2, приведенная ко входу схемы рис. 10.18, образуется параллельным соединением индуктивностей, определяемых выражениями (10.3) и (10.7) при замене входящих в них я соответственно на (я/2) + 1 и (я/2)-1. В результате при идентичных ЭТЛ, пользуясь (10.4) и (10.8), находим, что

12 = 121/я (я2-f 2). (10.12)

* Если X = nl2, то Lj , увеличивается на единицу за счет возрастания продольного напряжения на дополнительной линии.

Если линии с равными продольными напряжениями намотаны на общих магнитопроводах (совмещенная намотка), то при идентичных ЭТЛ величина Ls определится из (10.8) при замене п на п/2 и составит

и = 24L i (п + 1) (72 + 2).

(10.13)

Сравнивая (10.12) и (10.13) с (10.4), определяем выигрыш в величине Ls, равный соответственно

2 (п - 1) (2п - 1)/ (п^ Н- 2) п 4 {п - 1) {2п 1) / (п + 1) (п + 2).

При нечетных п величина Ls = Lsmax, если х = (п - 1)/2, и при идентичных ЭТЛ равна половине величины Ls, определяемой из (10.8) после замены в нем п на (п- 1)/2:

и = 12L/n (п2 + 1)*.

(10.14)

При совмещенной намотке линий с одинаковыми продольными напряжениями Ls увеличивается вдвое. Сравнивая выражения (10.4) и (10.14), находим выигрыш по Ls в 2 (2n - 1)/ (п + 1) раз. В ТЛ 1 : п при любом целом п

1 = 0

Для четных п и л; = п/2 f/ = (д^п, = n (л + 2)/4. Срав-

нивая это выражение с (10.8), получаем выигрыш в 2 (п + 1) X X (2n + 1)/{п^ + 2) раз. Величина шунтирующей индуктивности определяется из (10.12), а при совмещенной намотке - из (10.13). При нечетных п и х на интервале [ (п - 1)/2; (п + 1)/2]

f/вн = fB min (доп) = (tt + 1)/4.

При X = (n - 1)/2 сумма продольных напряжений на основных линиях будет минимальной, а напряжение на дополнительной линии станет равным ( + 1)/2. Величина Ls = Lsmax и определится из (10.14). При совмещенной намотке справедливо (10.8) с заменой п на (п + 1)/2 и составит La = 24L/ (п + 1) (п + 2) (п + 3).

ТЛ на одном магнитопроводе. Сравним ТЛ с дополнительной линией и без нее, выполненные на идентичных магнитопроводах (одном для каждого ЭТЛ). Принимая одинаковыми (при равных п) общие длины линий сравниваемых ТЛ, находим отношения результирующих величин шунтирующих индуктивностей.

Так, для ТЛ 1 : п без дополнительной линии суммарная длина линий, связанных с магнитопроводом, составляет

* При неизменной общей длине намотки, распределенной между отдельными элементарными узлами пропорционально продольным напряжениям на них, величина Z-j. одинакова для всех х = [{п - 1)/2; {п - 3)/21.

а для ТЛ 1 : -п

к^СУ i = /oM(/i-l)/2,

1п = 1оЪ г = /оп(/г + 1)/2.

(10.15) (10.16)

В обоих Случаях /о - длина линии с продольным напряжением U. При четных п для ТЛ 1 : п с дополнительной линией (рис. 10.17)

/ =/0

(п/2)-1

n/2-l

п/2 i = 1

= /o[n(n-f2)/4-l]. (10.17)

Приравнивая выражения (10.15) и (10.17), находим, что для ТЛ \:п отношение длин IJIq = р (или отношение чисел витков на напряжение И) составляет р+ = 2п {п - 1)/ (п^ + 2п - 4). При четных п для ТЛ 1 : -п величина р = 2 (л + l)/(n -f 2). При нечетных 3 аналогичный расчет с использованием выражений (10.15) и (10.16) дает

р+ = 2п/ (п + 3) и р = 2п/ (п + 1).

Отношение величин шунтирующих индуктивностей равно квадрату соответствующих значений р.

Помимо выигрыша в величине шунтирующей индуктивности и соответствующего расширения полосы в сторону нижних частот, уменьшается индукция (а следовательно, и потери) в магнитопроводе, благодаря чему допустима большая передаваемая мощность.

Введение дополнительной линии положительно проявляется и в области верхних частот при исключении фазокомпенсирующих линий. В этом случае имеет место меньшее рассогласование ввиду меньших длин линий. При четных п для ТЛ с дополнительной линией матрица [Hh в соответствии (x-n+f) Р^- 10.18 равна сумме матриц

(10.10) и (10.11), в которых следует заменить п на п/2.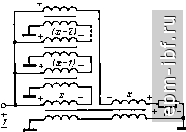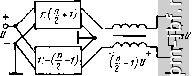

Рис. 10.17. Общий вид схемы ТЛ I : я с дополнительной линией Рис. 10.18. Функциональная схема ТЛ I : я с дополнительной четных п

линией прн

Полагая И7 = 1, находим, что входное сопротивление ТЛ с понижающей стороны при нормированной, равной п, нагрузке с повышающей стороны составит

n + im

2 [cos-i t Xo +C0S-1 (n - i) Xo] г = I

irfi-\- jnm

где

/п= 2 [tgfo + tg(/i-О^о].

1= 1

При нечетных п результирующая матрица [Я]2 также равна сумме матриц (10.10) и (10.11), но в первой из них следует заменить п на {п + 1)/2, а во второй - на (/г - 1)/2. В этом случае

вх н

n + i2mi

(n-I)/2

1 +2 2 о^-

- -1- /2remi

где

(n-I)/2

i= I

Соответствующий коэффициент отражения (по модулю) резко возрастает с увеличением х (рис. 10.19). Используя результаты расчета коррекции, полученные в § 10.3, можно уменьшить \ S \ для рассматриваемых ТЛ.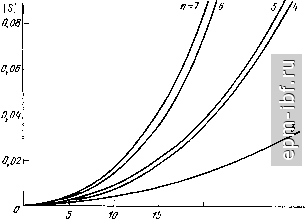

Рис. 10.19. Графики зависимостей <S=/(x) для ТЛ, изображенного иа рис. 10.18

10.5. КАСКАДНОЕ СОЕДИНЕНИЕ ТЛ

Рассмотрим частный случай - ТЛ 1 : 2* (рис. 10.20) , образованный каскадным соединением нескольких ТЛ 1 : 2, начиная с области нижних частот. Если все ТЛ 1 : 2 выполнены на раздельных магнитопроводах и имеют индуктивности (i = 1, 2, 3, k), то в соответствии с (10.3) результирующая шунтирующая индуктивность на понижающей стороне каскадного соединения составит k

Llk) =2 iVLi. Если все Li одинаковы, т. е. Li = Lq, to Lik) =

= 3Lo/(4* - 1) = 3Lo/ (ti - !) Сравнивая с (10.8), получаем U(k)/U = n(n + 2)/4 (ti - 1).

Если все ТЛ 1 : 2 содержат идентичные магнитопроводы, а числа витков линии прямо пропорциональны продольным напряжениям, то Ls(ft) = L/fe, где L - индуктивность проводника линии с Unp = U. Для каскадного ТЛ 1 : 2* величина U = 2>-\=n-I = f/BHmin-Она является минимальной, поскольку равна U для схемы 10.10.

При анализе области верхних частот заменим линию на магнитопроводе каждого ТЛ 1:2* согласно рис. 10.5, б. Теперь для ТЛ 1:2*, выполненного на одном магнитопроводе (или на идентичных магнитопроводах с одинаковой индукцией), просто составить матрицу а-параметров в виде произведения матриц, отвечающих составляющим ТЛ 1 : 2. При замене проводников всех фазокомпенсирующих линий непосредственными соединениями получим

21 22

= п

(1 -!g2 /а:о/2)/2 /4*-1 Г fg /хо/2

;4(i/ft-i) r-4g(A:o/2 2

где Хо - электрическая длина линии ТЛ 1 : 2 с f/H =

Входное сопротивление с понижающей стороны при подключении нагрузки nWI2 с повышающей стороны определяется выражением ZgxH = (%1 + 2ai2)/(a2i + 2а22) и соответственно \S\ = \Z- WI2 \1\ + WI2 I, что иллюстрируется рис. 10.21. Рассогласование существенно уменьшается, если осуществить коррекцию в соответствии с рис. 10.15.

- 2-V +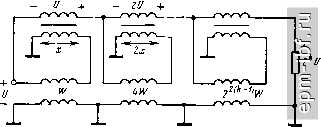

Рис. 10.20. Каскадное соединение, образующее ТЛ 1:2