трансформация. Так получаются ТЛ 1 : п с п = 2, 3, 5, 8, 13, 21 и т. д. Эти числа вместе с двумя исходными единицами, обусловленными первыми участками обеих линий, образуют известную последовательность Фибоначчи [31], и поэтому такие суммирующие ТЛ 1 : п будем обозначать ТЛФ 1 : п. Продольные напряжения на участках линий ТЛФ 1 : п, размещенных на магнитопроводе, также образуют последовательность Фибоначчи. Полученный результат может быть сформулирован как теорема. Теорема 11.2.

Наибольший целый коэффициент трансформации f суммирующего ТЛ (1 : п) с f/a = LjjH содержащего т участков линии, размещенной на магнитопроводе, есть [т + 2)-й член последовательности Фибоначчи, а нормированные продольные напряжения на участках составляют т первых членов этой последовательности.

Выигрыш по числу участков (но не по их неизменной суммарной длине) и разбросу номиналов волновых сопротивлений существенно возрастает с увеличением п. При любом п, не являющемся числом Фибоначчи, токи и напряжения в каждой из линий следует суммировать не поочередно. Так можно образовать ТЛ 1 : п с минимальным числом участков линий при уменьшенном разбросе номиналов их волновых сопротивлений*. Все вышесказанное относительно ТЛ 1 : п переносится и на ТЛ 1 : -п с учетом того, что ТЛ 1 : -п с Umimin образуется из соответствующего ТЛ 1 : п при введении дополнительного согласованного ЭТЛ с А^Уа = 1.

ТЛ +(1: л) можно образовать согласно рис. 10.12, использовав в качестве составляющих идентичные ТЛФ 1 : п. Если снять ограничивающее условие - наличие физической земли по оси симметрии, как это имело место для схемы рис. 11.5, то осуществимо дальнейшее сокращение числа участков линий. Примером служит схема рис. 11.11. Она имеет при большом коэффициенте трансформации небольшой разброс величин волновых сопротивлений: {W} = = {1/4, 1/3, 1, 3, 4}, т. е. общее отношение равно 16 (как и для ТЛФ 1:4).

Обеспечивая на каждом стыке участков наибольшую сумму напряжений, т. е. наибольший коэффициент трансформации (рис. 11.12), получим такую последовательность коэффициентов трансформации:

3, 5, 11, 19, 41, 71, 153, 265, ... (11.4)

Правомерна и другая последовательность (рис. 11.13):

3, 5, 9, 19, 33, 71, 123, 265. (11.5).

Обе они возрастают быстрее последовательности Фибоначчи, совпадают между собой в членах с четными порядковыми номерами (исключая общий первый член) и могут быть выражены однотипными

♦ Не изменяя работы любой из рассмотренных схем с двумя линиями, можно перенести магнитопровод из верхней линии в нижнюю, а заземляемые зажимы наоборот.

рекуррентными соотношениями. Дополнив последовательность (11.4) слева двумя единицами, получим

п„+а = ft+i + 2пй (11.6)

для ее нечетных членов и

пл+з = %+2 + ft+i + Пй (11-7)

для четных членов, полагая ni = = \; k = \, 2, 3, ... Если последовательность (11.5) дополнить слева одной единицей, то окажутся справедливыми (11.6) и (11.7) при условии, что % = 1, Пг = 3.

Если коэффициент трансформации не является членом последовательности (11.4) или (11.5), то подобно ТЛФ 1 : п с п, отличным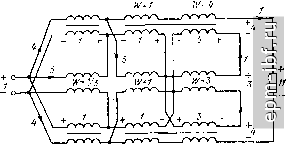

Рис. 11.11. Схема ТЛ +(1 : И)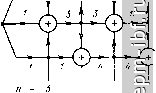

5 11 13 1*1 11 155 165 Рис. 11.12. Структура схем ТЛ ±(1 :/г) с максимальной трансформацнец

31 Э7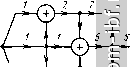

07 7 15 IB э;

7Г

л 5 5 9 19 ЗЪ 11 125 265 Рис. 11.13. Структура схем ТЛ ±(1 : п)

от числа Фибоначчи, можно получить схему с наименьшим числом ступеней. Нужно лишь выбрать соответствующую последовательность суммирования напряжений. При этом нельзя утверждать, что решение единственное. Из рис. 11.12 и 11.13 видно, что поскольку в каждой ступени трансформации использованы все три линии, то независимо от последовательности суммирования, коэффициент трансформации есть нечетное число. Если коэффициент трансформации выражается четным числом, то средняя линия может быть исключена на какой-либо ступени трансформации, например на последней. При этом коэффициент трансформации становится большим поочередно для обоих вариантов схем. Если исключить первый участок средней линии в структуре рис. 11.12, то = 2*, где h - число ступеней.

Изложенный в настоящем параграфе метод построения ТЛ с уменьшенным (в том числе минимальным) числом участков линий применим и к гальванически развязанным ТЛ типа рис. 11.8.

П.З. АНАЛИЗ ТЛ ПРИ ВАРИАЦИЯХ ПАРАМЕТРОВ

Часто бывает желательно упрощение конструкции ТЛ путем исключения фазокомпенсирующих линий, использования более ограниченного набора величин волновых сопротивлений и т. д., допустив при этом некоторое рассогласование в области верхних частот. Рассмотрим частные случаи.

I. Прн нсключеннн всех фазокомпенсирующих линий схемы рис. 11.1 и 11.3 становятся тождественными. Тогда проводимость с понижающей сто-п т

роны Tji г/вх = (1/) 2 2 hh- где /j-ток, протекающий в короткозамкну-

той k-u обмотке прн действии источника U только на (-й обмотке.

Здесь предполагается, что все параллельно соединяемые п - 1 обмоткн разделены и к каждой из них подключен источник с напряжением U. Результирующий ток определяется от воздействия всех источников*. Иными словами, г/вн есть сумма всех элементов матрицы проводимостей рассматриваемой ценн, записанной относительно п раздельных входов (обмоток), параллельное соединение которых образует вход ТЛ с понижающей стороны.

В простейшем случае, когда волновые сопротивления участков равной длины одинаковы и равны, в частности, сопротивлению нагрузки R с повышающей стороны**, матрица R имеет элементы (г, k = 1,2, л), равные

г/гй= [ехр(-/[((, k} ,- 1] х)] cos [{(, k} -\]x, где X- электрическая длина каждого участка линии.

* Суммирование в формуле для г/в^ осуществляется без изменения знака перед величинами 7, при ( Ф k, поскольку при переходе от одного входа к другому направление тока изменяется на обратное.

** Такой ТЛ с однородной линией известен в различных конструктивных вариантах [20, 33, 35). Прн малых величинах нагрузочных сопротивлений хорошие результаты получаются с обмоткой из кабеля, внешний проводник которого, составляющий понижающую обмотку, разделен после каждого витка и объединен объемным витком.

Модуль коэффициента отражения

i, ft= i

i,k = i

иллюстрируется зависимостью / на рис. 11.14.

2. Более общий случай, также при условии, что х^ = х^ = Хц = ... = = а: = О, а = X, но отвечающий неравным нормированным (относительно нагрузки с повышающей стороны) величинам волновых сопротивлений участков линий, иллюстрируется остальными зависимостями на рис. 11.14. Численные расчеты производились на ЭВМ для общей схемы (рис. 11.15) в такой последовательности:

All Ml

/,(3) /,(3) 12 22 -

в

22 J

L 1/aiV

(5 )/ (5)

12 / 11 ,

MV /4VJ

(9) 12

->

В

n= 3

aiV/a[\>

- 12 / 11 -

1- Ml

В

n = 4

IMV лт) 411. 1 га<\2, 4i2>

(13) 12

(13> 22 J

B-1 И. T. Д.

Символы В и S-i означают переход от матрицы Л-параметров к матрице а-параметров, и наоборот. Элементы матриц [Н] и [А] для входящих в ТЛ отрезков однородных линий таковы*:

=/Гг1 tg х , . AiV-= 1/C0S Х(1,. ,2>;

/tV-2> = /ritgx,i ,2 ед-<1 - .....=/H7rMg,3 (4 <5>.....;

й^6> 10 (14 ...,=l/coSX(3>,-,4 ,5

= -/4itg*:,3> 4 а[\), (8), (12), ...,=cosxi, ait

/(6),(10), (14), ... - ... 22 -

(6),

=/l(2>,(3),(4>.....SinXi,

V .....=/й7,2),(3),(4>,...,5ШХ1.

* При определении всех элементов положительные направления токов приняты входящими в четырехполюсники на их входах н выходящими из них на выходах.

Модуль коэффициента отражения рассчитывался по формуле

\S\ =

где = (4/г - 3) - порядковый номер результирующей 2Р-цепи при л > 2.

При расчете зависимостей \S\ = / (х) для ТЛ 1 : п предполагалось, что нагрузка на повышающей стороне, равная единице, подключена к линии с волновым сопротивлением Wn = Кроме того, принималось Xi = х, а х^ Хз = = Xi ... = Хп = О, т. е. исключены все фазокомпенсирующие линии.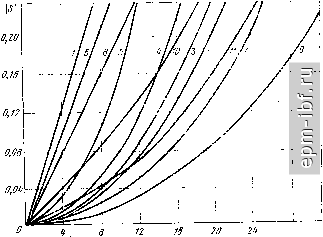

г 8 в,гра^

Рис. 11.14. Расчетные зависимости S=/(x) для упрощенных ТЛ 1 : п при различных наборах величин W:

1172=0,25, 1!7з=0.5, \\з=1; 9) 7,-те же, что у схемы рис. 11.3;

п=6: /) 117,-117з = 1; 2) 117,-1175 те же, что у схемы на рис. П.З; 3) 117, = 1172= ------ .

Й7,= 1175 = 0,75; 4) Ц7,-и7з = 0,375, 1174=1173 = 0,75; 5) №',-1175=0,5; /1 = 5: 6) 117,-117,= I; 1) 117,-11/4

те же, что у схемы рис. 11.3; /1=4; s) 10) 117,-Й7з=0,75; ) U7, = ll72=I/3, Ц7з = 2/3

г

I

I

J

?5 /7-5l

J

J

hn-i

Рис. 11.15. функциональная схема ТЛ 1 : п 188

С помощью сосредоточенных корректирующих элементов, включённых согласие рис. 10.15, можно существенно снизить коэффициент отражения. Наконец, в § 11.7 будет показано на ряде примеров, что коэффициент отражения можно сделать тождественно равным нулю, если каждую линию выполнить двухступенчатой.

3. Рассматриваемые в § 11.2 ТЛ 1 : п можно упростить, например за счет сокращения номенклатуры величин волновых сопротивлений участков линий. Для определения возникающего при этом рассогласования воспользуемся матрицами \А\ составляющих цепей (рис. 11.10), связывающих переменные на одной их стороне с переменными на другой:

где матрицы

О

о

12 (2) 22 (2)J

\\ (1) 4<1,

11 (2)

41 а,

о

О

О

о

И (2) 21 (2)

12 (1) 2 2 (I) 12 (2) 22 (2) 1

относятся соответственно к первой и второй (изображенной частично) схемам рис. 11.10. Элементы этих матриц есть, в свою очередь, элементы [Л] матриц отрезков одиночных линий, а в общем случае - составляющих 2Р-цепей. Матрицы [i4]* и [i4]* перемножаются в порядке каскадного включения составляющих цепей, образуя [Л]-матрицу результирующей (2Х 2) Р-цепи.

Для перехода к [Л]-матрице четырехполюсника (т. е. ТЛ 1 : л) с элементами Оц, 012, 221 и воспользуемся граничными условиями: t/i= IJ\ = L 2 , h = + f2 ДЛЯ любой из схем рис. 11.10 и = Uf\ =

Z*, * = О или (Уа = и[ К /2 = 1[ К /<з = О для первой и второй соответственно; т - последняя из этих схем.

Коэффициент отражения для нормированных схем рассчитывается по формуле

о а22~п^ ац+п (021-012)

022+rtail+n (021 + 012)

Результаты численного расчета (рис. 11.16) указывают область использования упрощенной конструкции.

4. На практике широко используется автотрансформатор типа рис. 11.17 с коэффициентом трансформации в общем случае n = m/{m~k), выполненный в виде /и-витков плоской спирали, охватывающей магнитопровод и имеющей отвод от конца k-то ее витка для подключения нагрузки [84, 87]. Так как

Цифры в скобках (1) и (2) характеризуют о-параметры для линий с волновыми сопротивлениями и WW соответственно.