X и обращается в нуль при х = 90°.; оно существенно возрастает только при X > 90°.

2. Схема ТЛ 1 : 5/2 (рис. 11.23) содержит линии двух номиналов волновых сопротивлений. Два участка линий (2х), не связанные с магнитопроводом, эквипотенциальны. Их можно объединить в один с нормированным волновым сопротивлением, равным 2/3.

Рассмотренный выше метод синтеза, основанный на разложении величины п = pIq в цепную дробь, является не единственным,

обеспечивающим f/Bumln-

Другой метод основан на представлении величины п = p/q в виде п = Пд + k/q, где - наибольшая целая часть дроби, а k- числитель ее остатка. На первом шаге синтеза можно реализовать, например, минимальную повышающую трансформацию (рис. 11.24, а), т. е. величину 1 + \/q ценой А^/витш - 1- Затем следует вводить в определенном порядке напряжения из одной линии в другую до тех пор, пока сумма напряжений в обеих линиях не составит p/q. В общем случае порядок суммирования не является единственным. В частности, если p/q - а -\- b/q, где а я b есть соседние члены последовательности Фибоначчи, то можно поочередно вводить напряжения из одной линии в другую; это дает наименьший разброс величин волновых сопротивлений участков линий. Крайний случай реализации рассмотренным методом состоит в выделении на первом шаге величины Пд + i/q ценой А^/внтш = о (рис. 11.24, б). На каждом из последующих к- 1 шагов добавляется величина l/q за счет А{/внт1п= Ч-

При любом порядке суммирования всякий раз на введение того или иного напряжения, составляющего линейную комбинацию величин 1 и \/q, расходуется равное ему Af/aHmin- результате, суммируя всегда величины Аиа= и p/q - {q + \)/q, получаем (11.10).

Пример. Схема рис. 11.25 (или дуальная ей, имеющая {W} = {1;2/3; 2}) может оказаться более удобной для выполнения, чем схема рис. 11.23 или дуальная ей с {W} = {1; 1/2}.

Сравнивая параллельно-последовательную и ступенчатую реализации, отметим, что они различаются по своей сути тем, что в первой из них знаменатель дроби q реализуется на протяжении всех шагов, а во второй - на первом шаге. Это приводит к тому, что при параллельно-последовательной реализации оказывается меньшим разброс номиналов волновых сопротивлений, однако структуры менее удобны для практического выполнения. Оба изложенных здесь метода применимы и для ТЛ типа ±(1 : п) с /внт1п (Р - Простейшим примером служит схема с единым номиналом величин волновых сопротивлений всех участков линий (рис. 11.26). Согласованные ТЛ 1 : -п с f/aHmin из (И.И) образуются, как упоминалось выше, из ТЛ 1 : п путем добавления на его понижающей стороне ТЛ 1 : -1.

Симметрирующие ТЛ 1 : ± /2 можно реализовать не только согласно схемам рис. 10.28, б путем внутреннего каскадного соеди-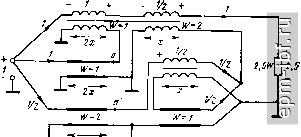

Рис. 11.23. Схема ТЛ 1 :5/2 с Увн = {/вн min = 2

т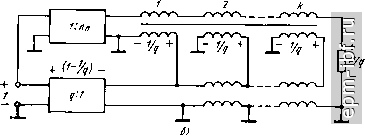

Рис. 11.24. Ступенчатая реализация ТЛ 1 : п с Umi min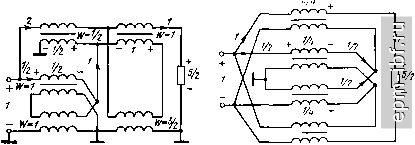

+ г/> -

Рис. 11.25. Схема ТЛ 1 : 5/2 с /вн mm

Рис. П.26. Схема ТЛ ±(1 : 5/2) с (;внт1п = 2

нения, что в конструктивном отношении может оказаться малопригодным. Другой метод реализации [88] дает в сравнении с (11.12) меньшие значения U и равные

t/вн = (Р - 3/2)/(7 + 1/2.

(11.13)

На первом шаге его реализации, обобщающей случай целых п, в частности схемы рис. 11.7, а, б, осуществим симметрирование и минимальную повышающую трансформацию (рис. 11.27, а, б), т. е. образуем ТЛ 1 : ±((7 + l)/q. На это расходуется

At/bhrnini =iQ- т + 1)/2<? = {3д- l)/2q. (11.14)

Последующая трансформация от величины {q + 1)/ до p/q достигается за счет

А^/знш,п2 = р/7-(<7+(11-15)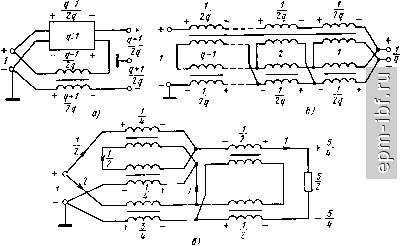

Рис. 11.27. Первая (симметрирующая) ступень реализации ТЛ 1 : ± /2 с {/внтш (а), возможная реализация ТЛ \ : q (б) и схема ТЛ 1 : ±5/4 с Ubb min (в)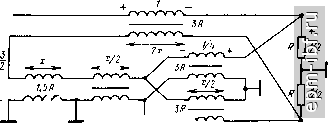

+ /Л -

1 г

+ fA -

Рис. 11.28. Схема ТЛ 3/2 : ±1/2 с уменьщенной асимметрией 198

и реализуется ступенчатым суммированием. На каждом шаге его добавляется линейная комбинация величин 1 и l/q за счет равного ей А t/вн min-Складывая правые части выражений (11.14) и (11.15), получаем (11.13)*. Примером ТЛ 1 : ±/i/2 при п = 5/2 является схема рис. 11.27, в. Как и для ранее рассмотренных ТЛ, за счет небольшой избыточности в f/вн можно уменьшить существенно разброс величин волновых сопротивлений участков линий.

Для ТЛ я: ±1/2 при любых п > 1 также существует реализация [88], отличающаяся от варианта рис. 10.28, в, первый шаг которой обеспечивает переход к несимметричному относительно земли напряжению при минимальной повышающей трансформации (в 1 + + l/q раз). На это расходуется

Ai/B mln = 3/2.

(11.16)

Оставшаяся трансформация та же, что и после первого шага реализации ТЛ 1 : ±я/2, согласно [88] достигается аналогичным путем и за счет At/ghmin из (11.15). Суммируя правые части выражений (11.15) и (11.16), получаем (11.12).

Как уже отмечалось ранее, симметрирующие ТЛ с t/enmin обладают заметной асимметрией. Ее можно существенно снизить, если допустить небольшую избыточность в (/вн- Примером служит схема рис. 11.28.

11.5. КАСКАДНАЯ РЕАЛИЗАЦИЯ ТЛ

Рассмотрим каскадные реализации, основанные на представлении величины п (целой или дробной) различными сомножителями,

в том числе и дробными, при которых сохраняется (/вн = внтШ-

Найдем такие сомножители сначала для ТЛ 1 : я, для чего представим я в виде двух сомножителей:

п = р/д = (Рг/Чг) (рШ (11-17)

В соответствии с (11.10)

ви min = (P1P2 - l)/flifla- (11.18)

Определим, при каких соотношениях натуральных чисел р^, р^, <7i и 7а может быть образовано каскадное соединение двух ТЛ с

tbh = t/вн min- Предположим, ЧТО

piXi 1, Рг>д2> 1- (11.19)

Тогда (/вн = (Pi - l)/qi + (Pi/?i) (Ра - l)/fl2- Сравнивая это выражение с (11.18) находим

А(/в„ = t/вн - iBH min = (Pi - 1) (72 - l)/7i7a. (11-20)

* При ограниченных величинах п., например при п - p/q > 2 к р, имеющем делитель k такой, чтобы pik > о, каскадное соединение ТЛ 1: p/kq и ТЛ 1: ± k/2 дает (11.10).

Отсюда видно, что AU = О только при 2=1, поскольку = = О не удовлетворяет условию (11.19). Иными словами, Usamin обеспечивается только каскадным соединением ТЛ в соответствии с разложением

п = p/q = рхр^/д. (11.21)

Аналогично можно показать, что при

Pi>gi>i, 1 <Р2 <72 (11.22)

1 <Pi<7i, P2>Q2>i (11.23)

или

/вн>0. значит, образование ТЛ с t/ehmin согласно (11.18) невозможно.

Поскольку ТЛ ± (1 : п) всегда можно образовать из двух идентичных ТЛ 1 : п, мы вправе сформулировать следующую теорему. Теорема 11.4.

ТЛ на согласованных двухпроводных линиях с любым несократимым п p/q> 1, симметричные и несимметричные относительно земли с обеих сторон (без изменения полярности в последних) реализуются при t/вн min каскадным соединением в соответствии с любым разложением вида:

= (pi/q)p2P3PiP5pe - при pi > 7 > 1.

(11.24)

Рассмотрим ТЛ 1 : -л. В этом случае в соответствии с (11.11) и (11.17)

t/shmin = (P1P2 - l)/7l72 + 1. (11.25)

Если полярность изменяется на понижающей стороне ТЛ, которому соответствует первый сомножитель в (11.17), и выполняется условие (11.19), то согласно (11.10) и (11.11) U = (р^- l)/</i + + 1 + (pi/qi) (р2 - O/z- Сравнивая это выражение с (11.25), находим, что А^/вн снова определяется из (11.20), т. е.ТЛ 1 : - п при условии (11.19) также можно~ реализовать с t/anmin только в соответствии с разложением (11.21). Если полярность изменяется во втором из каскадно включенных ТЛ, то

= (Рг - mi + (PifQi) НР2 - Щ2 + 11

и

AtBii = [(7i - 1) (Pi - 1) + 72 (pi - qi)Vqig2,

т. e. At/вп > 0 и, следовательно, в этом случае t/gHmin недостижимо.

Аналогично показывается, что при условии (11.22) А(Ув >.0 вне зависимости от того, в каком из ТЛ изменяется полярность. Предположим теперь, что выполняется условие (11.23), а полярность изменяется на понижающей стороне ТЛ с = pj/j. В этом случае = (Pi/i) (Й! - 1)/Pi + 1 + (piJqi) (Pi - 1)/?2- Сравнивая это выражение с (11.25), снова получим (11.20). При изменении по-

лярности на понижающей стороне второго ТЛ величина t/g определяется выражением, аналогичным последнему. В результате справедлива следующая теорема. Теорема 11.5.

ТЛ 1: -п на согласованных двухпроводных линиях с любым несократимым п = p/q > 1 допускают при (/в„ каскадную реализацию по теореме 11.4 и разложению(11.17), если pi = 1 п (или) q2=l, а полярность изменяется с понижающей стороны любого из составляющих ТЛ.

Частным случаем теорем 11.3 и 11.4 при q = 1 является теорема 11.6.

Теорема 11.6.

Симметричные и несимметричные относительно земли с обеих сторон ТЛ на согласованных двухпроводных линиях при произвольном целом п допускают каскадную реализацию при t/вн min любому разложению п = п^п^п^ с целыми сомножителями, только первому из которых может соответствовать ТЛ, изменяющий полярность.

Действительно, если при п = р^ полярность изменяется в первом ТЛ, то t/вн = Pi + Рг (р2 - 1) = Ргр2 = п = и

вя min>

во втором, то t/вн = Pi - 1 + Ргр2 > вн min-

Для симметрирующих ТЛ, выполненных согласно рис. 10.28, допустима каскадная реализация входящих в них ТЛ 1 : л и ТЛ 1 : -л в соответствии с вышеприведенными теоремами. Ранее было показано, что если допустить избыточность в (/в„, т. е. принять fbh > fbh min> МОЖНО сократить номенклатуру величин волновых сопротивлений линий и упростить конструкцию ТЛ. При этом резко возрастает количество возможных вариантов. Отметим некоторые из них применительно к ТЛ 1 : л.

В отличие от ТЛ 1 : л с двумя линиями (§11.1 и 11.2), примем в качестве элемента три линии (рис. 11.29). В этом случае t/вн = = % tbhrnin коэффициент трансформации после й-й ступени составит Пи = 2лй 1 +1, Ло = 1, где = 1, 2, 3, ...

При использовании в ступенях параллельно-последовательных ТЛ 1 : (л - 1) нетрудно получить л^ = (л - \)пи-г + 1, где Ло =

= 1. k=\, 2, 3, а t/3 = t/bhmia[l/( -l)rjt=nt/bhmla/2.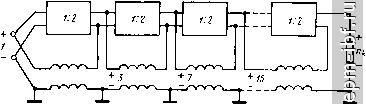

Рис. 11.29. Функциональная схема ТЛ 1 :п с £/вв>/внт1п