Можно использовать в ступенях и другие ТЛ, в частности имеющие структуры, рассмотренные в § 11.2, а также ТЛ с различными коэффициентами трансформации и т. д. При этом всегда можно оценить целесообразность использования той или иной схемы, имеющей

вн вн min-

И.6. ТРАНСФОРМАТОРЫ НА МНОГОПРОВОДНЫХ ЛИНИЯХ

- Расщиренную полосу частот, больший к. п. д. и меньшие габариты имеют ТЛ с целыми и дробными п, если их выполнить на многопроводных линиях. Простейший, но важный частный Случай ТЛ 1 : 3/2 (рис. 11.30, а) содержит спаренные коаксиальные линии и работает следующим образом [92, 94]. На нижних частотах, когда электрические длины линий пренебрежимо малы и единственным реактивным элементом схемы замещения ТЛ является его шунтирующая индуктивность, имеем обычный автотрансформатор, образованный тремя проводниками: двумя внутренними проводниками верхних линий и внешним, объединяющим их.

В основном рабочем диапазоне можно пренебречь шунтирующей индуктивностью и работа трансформатора определяется процессом прохождения колебаний по всем его линиям равной электрической длины. Входной сигнал амплитудой 2U поступает одновременно в обе линии с волновым сопротивлением 2W и делится поровну между двумя аналогичными линиями с волновым сопротивлением W. В результате для падающей волны входное сопротивление с понижающей стороны составит 2W/3, а поступившие в линии колебания доходят до их выходов и там попарно синфазно суммируются, давая в сумме Ъи. Чтобы это напряжение без отражения поступило в нагрузку, ее величина должна быть 3W/2.

В результате получим согласованный ТЛ 1 : 3/2, более простой, чем ТЛ (рис. 11.20, а), и с относительно большей шунтирующей индуктивностью. Оба эти факта обусловливают упомянутые выше достоинства ТЛ на многопроводных линиях.

Вышеизложенное в равной степени относится и к рис. 11.30, б - схеме, эквивалентной рис. 11.30, а. Существует множество эквивалентных схем, синтез которых основан на следующем. Спаренные коаксиальные линии схем на рис. 11.30, оторванные от земли, представляют собой частный случай трехпроводной линии, каждый

- т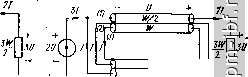

7 /:

Рис. 11.30. Схемы ТЛ 1:3/2 с различными величинами волновых сопротивлений линий

проводник которой имеет нулевую проводимость относительно обратного токопровода - земли*. Матрица волновых проводимостей такой линии связывает амплитуды токов и напряжений бегущих волн в системе уравнений:

(11.26)

где Gi3= \I2W, G12 = \IW, g23 = О для схемы рис. 11.30, а и = 21W, g23 = \IW, Gi3 = О для схемы рис. 11.30, б. Полагая W = \ п U = \ нормированными для схемы рис. 11.30, а, получим / = 1, т. е. на повышающей стороне токи в проводниках и напряжения на них относительно земли составят: /1 = 2, /а = = /3 = -1, t/i = 3, (/2 = 2, t/3 = 1. Поскольку волновая проводимость каждого проводника относительно земли принята равной нулю, матрица [G] - вырожденная (det [G] = 0), а система уравнений (11.26) - неопределенная. Это означает, что, помимо найденных частных решений, для элементов матрицы [G1 существует множество других, при которых схемы ТЛ 1 : 3/2 также будут согласованы. Для их отыскания обозначим

Gi2 = feGi3

(11.27)

и подставим это условие в развернутые выражения системы (11.26) В результате расчета получим G12 = 2klW (k -f 2), g13 = 2/(k + + 2)W, G23 = {k-2)/ (k + 2)W.

Из условия физической реализуемости матрицы [G], выражаемого в данном случае как Gj 0; i Ф т; i, т = 1, 2, 3, находим 2 < оо. Условию k = 2 отвечает схема рис. 11.30, а, ak = сх - схема рис. 11.30, б. При промежуточных значениях k все три проводника связаны между собой. В частности, при = 4 трехпровод-ная линия обладает симметрией: G12 = i/3W, g13 = g23 = 1/31.

Рассмотренный принцип построения ТЛ 1 : 3/2 распространяется на общий случай ТЛ \ : (N -{- l)/N (рис. 1Г31), а для отыскания эквивалентных схем справедлив вышеизложенный метод. Вначале определяется число свободных неизвестных (или дополнительных соотношений между элементами матрицы [G] ):

N {N + 1)/2 - N = N{N - 1)/2,

где N (N + 1)/2 - общее число неизвестных параметров матрицы [G], - ранг матрицы [G]. Далее составляется система уравнений по типу (11.26), в которую вводятся эти дополнительные условия. Их удобно выразить независимыми соотношениями типа (11.27), свя-

* Это строго справедливо для двух экранированных проводников и при соответствующей конструкции-с достаточной степенью приближения для экранирующего проводника.

** Порядковые номера проводников указаны в скобках иа рис. 11.30.

зывающими элементы матрицы [G] вещественными неотрицательными коэффициентами i, 2> > N(N-i)/2-Решением системыурав-нений определяются выражения для остальных элементов матрицы через эти коэффициенты.

Условие физической реализуемости матрицы [G], состоящее в том, что она должна быть гипердоминантной [91], накладывает определенные ограничения на коэффициенты ki, k, kg, к^(ы-\)12, выражаемые системой линейных неравенств. Так, например, при N = 3 имеем

и примем Gi3 = kfix2, Gik = 212. G23 = kGi- Подставляя эти выражения в развернутые уравнения системы, получаем общие выражения для элементов матрицы [G] : Ga = 3/а, G24 = (2 - - 2A:i-32 -Зйз)/2а и G34 = (41 - Зк + Зк- 1)/а, где а = = (1 + 2кг + 3k2)W.

Условие физической реализуемости матрицы [G]: 2 + 32 + -f З^з < 2 и 41 - 32 + 33 > 1. Решение, отвечающее схеме рис. 11.31 для N = 3, будет, если к- = 1/2, к^ = 1/3, йз = 0. Приняв, например, = fej = О, а з = 1/3 (или 2/3), получим другие эквивалентные схемы.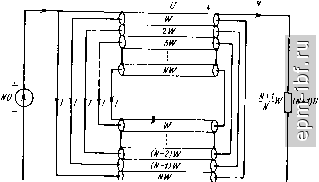

Рис. 11.31. Общий вид схемы ТЛ 1 : (N+\)jN

О

Уго

(1/3)

(1/S) (ji

-ш

г

Практическая реализация схем, в. которых связи между проводниками многопроводной линии не сводятся к набору волновых сопротивлений пар проводников, осложняется тем, что нет удобных методов расчета конструктивных параметров многопроводных линий по их матрицам волновых проводимостей.

Все вышеизложенное полностью относится и к ТЛ ±(1 : я), например, к схемам рис. 11.32, а, б, для первой из которых в скобках указаны относительные величины мощностей в согласованных лини-

Рис. 11.32. Схемы симметричных ТЛ:

а -частный случай ТЛ ±(1:3/2); б - поперечное сечение четырехслойного полоскового тл ±(1:4/3) при fe, = ft2=0. fo=2/3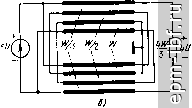

О

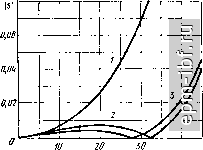X, граб

Рис. 11.33. Схема ТЛ +(1 : 5/3)

Рис. 11.34. Зависимости модуля коэффициента отражения для схем рис. 11.30 при исключении фазокомпенсирующих линий (кривая /) и при последующем введении корректирующих элементов (кривые 2 и 5): I) bi=0, 62=0; 2) bi=0,5675, 62=0,4944; 3) Ь,=0,5416, Ь2=0,4953

+ и/г

Рис. 11.35. Схемы симметрирующих ТЛ: а-ТЛ 1 : ±1: б-ТЛ 1 : ±3/4

ях. Эти схемы, дуальные для соответствующих схеме рис. 11.31, в симметричном варианте обобщаются на произвольное N при наборе величин волновых сопротивлений {W, WI2, W/3, WIN). Существуют и схемы для л > (Л^ + 1)/Л^, (см..например рис. 11.33).

При небольшой электрической длине линий для упрощения конструкции можно заменить проводники фазокомпенсирующих линий непосредственными соединениями. При этом для схем рис. 11.30, а, б возникает рассогласование (кривая / на рис. 11.34). Его можно уменьшить (см. кривые 2 и 3) введением корректирующих элементов: с понижающей стороны - шунтирующего конденсатора с емкостью С[пФ] = (WllklWQ), с повышающей стороны- индуктивного элемента L [мкГ] = (bi/3-lO)tt(Q)/, й (последовательно с нагрузкой), где / - длина каждой линии в метрах; k - коэффициент укорочения длины волны в линии.

В простейшем симметрирующем ТЛ (рис. 11.35, а) коаксиальная линия обеспечивает симметрирование, а внешняя поверхность ее наружного проводника вместе с компенсирующим проводником входят в ТЛ rt (1 : 2). В таком устройстве сочетаются высокая степень симметрии и простота конструкции.

Используя этот принцип внутреннего каскадного соединения ТЛ 1 : ±1/2 с симметричным ТЛ и принимая в качестве последнего ТЛ на многопроводных линиях, получим различные схемы симметрирующих ТЛ, например, рис. 11.35,6 для = 3/2 [99].

11.7. ТРАНСФОРМАТОРЫ С ПРЕДЕЛЬНО ШИРОКОЙ ПОЛОСОЙ ЧАСТОТ

Принципиальные ограничения обычных Тр обусловлены, как известно (§ 10.1), противоречивыми условиями минимизации интегральных параметров обмоток: индуктивностей рассеяния, собственных и взаимных емкостей. Вместе с тем, в таких Тр длины проводников используются наилучшим образом для получения требуемой индуктивности обмотки, следовательно, нижней граничной частоты; при этом достигается и минимальный габарит трансформатора.

В ТЛ, обмотки которых образованы отрезками согласованных двухпроводных (в том числе коаксиальных) линий передачи, соединенных между собой различным образом, реализуется расширенная полоса частот. Однако такие ТЛ в силу ограниченности их элементной базы (согласованных двухпроводных линий) имеют три существенных недостатка:

- суммарные напряжения на проводниках линий и длины по- , следних много большие, чем в обычных Тр;

- имеются дополнительные фазокомпенсирующие линии;

- расстояния между линиями должны быть относительно большими для исключения взаимосвязи.

Отмеченные недостатки приводят к увеличению габарита ТЛ, снижению его к. п. д. и сужению рабочей полосы частот. Они частич-

20в

НО устранены в ТЛ на согласованных многопроводных линиях (§ 11.6) и отсутствуют в ТЛ ± [1 : (iV + 1)1 N] (типа рис. 11.32), которые по структуре соединений проводников аналогичны обычным Тр.

Развивая далее принципы построения ТЛ, оказывается возможным сохранить достоинства обычных Тр и устранить упомянутые недостатки в согласованных ТЛ с произвольными коэффициентами трансформации и при различных включениях их зажимов относительно земли.

Рассмотрим новый принцип выполнения обмоток, состоящий в том, что проводники каждой из них образуют отрезок многопроводной линии, имеющей две равные по длине ступени при определенных соотношениях для их волновых проводимостей. Эти соотношения обеспечивают полное согласование в области верхних частот, где схема замещения ТЛ эквивалентна скрещенной цепи нулевого затухания с нелинейной, в общем случае, фазочастотной характеристикой 1з (х). При такой характеристике в линиях ТЛ нет режима бегущей волны, но сохраняется полное его согласование со стороны внешних зажимов*.

С использованием этого принципа выполнения обмоток ТЛ устраняются упомянутые недостатки известных решений при произвольных коэффициентах трансформации для различных включений обмоток относительно земли, а также сохраняются все достоинства простых Тр. В результате реализуются предельно широкая полоса частот и минимальные размеры ТЛ.

Расщотрим сначала ТЛ с несимметричными относительно земли входами (ТЛ 1 : п).

Простейшим и наиболее употребимым является ТЛ 1 : 2 с предельно широкой рабочей полосой частот (рис. 11.36), он имеет равные по длине ступени двухпроводной линии, размещенной на магнитопроводе**. Нормированное волновое сопротивление первой ступени (электрической длины х) составляет 1/КЗ, а второй (также длины х) равно КЗ. Нормировка производится к среднегеометрической величине номинальных сопротивлений с понижающей и повышающей сторон ТЛ. Этот ТЛ 1 : 2 имеет для области верхних частот эквивалентную скрещенную цепь нулевого затухания (рис. 11.36, б при п = 2), где 2 = Ц1УЩ tg х; фазовый сдвиг в трансформаторе определяется соотношением tg (г|;/2) = (1/3) tg х. На рис. 11.36, в приведен внешний вид такого ТЛ, имеющего два набора кольцевых сердечников. На повышающей стороне ТЛ установлен коаксиальный 75-омный разъем, а на понижающей - полоско-вый вывод. В диапазоне частот 3-300 МГц модуль коэффициента отражения не более 0,05.

* Аналогичная по смыслу ситуация имеет место в направленных ответ-вителях на связанных линиях.

** Здесь и далее на схемах магнитопровод не изображается.