в сравнении с классическим ТЛ 1 : 2 (рис. 10.8, а), состоящим из двух идентичных линий, соединенных с одной стор оны параллельно, а с другой последовательно, выданном ТЛ устранены все отмеченные выше недостатки.

Более сложным является ТЛ 1 : 3 (рис. 11.37, а)*, образованный, можно считать, из ТЛ 1 : 3 типа схем, показанных на рис. 11.1 или 11.4, при исключении всех фазокомпенсирующих линий с последующим объединением проводников, имеющих общие зажимы, и выполнении каждого участка основной линии двухступенчатым. Нормированные величины волновых сопротивлений ступеней (Wta, Wio) составляют:

Wa = (1 + I 2l)/10 2, Wi6 = (7 + 3 К2Г)/14]/2. Wa = (14 + 2V2\)nV2, W26 = 21 2.

Этому ТЛ 1 : 3 эквивалентна скрещенная цепь нулевого затухания (рис. 11.36, б при п = 3), в которой 2 - сопротивление двухступенчатой (pi; X, Ра; х) линии, короткозамкнутой на конце со стороны ступени (Ра; х). При этом = 2 {Wi+ Wie); p2=Wia(W2a + + W2,Wx6 + W. s{Wxa+ WisVwJ, a

Z= (3 400)0+/2irtgx = .tg(,/2) . 1- [(1+ /2T)/I00]tg=x

Более предпочтительным может оказаться ТЛ (рис. 11.37,6), также удобный для полоскового исполнения. Он является дуальным схеме рис. 11.37, а в области верхних частот и имеет ту же зависимость ф (х).

Для согласованого ТЛ 1 :3, выполненного в общем случае с использованием трехпроводной двухступенчатой линии, можно иметь различные варианты, отличающиеся величинами связей между проводниками линий в ступенях. При этом получаются и разные зависимости ф (х). Вариант с наиболее пологой зависимостью ф (х) предпочтителен, как правило, если предусматривается работа на рассогласованную нагрузку.

С помощью трехпроводной линии реализуется также ТЛ 1 : 3/2, в частности вариант (рис. 11.38, а), являющийся, как и ТЛ 1 : 2 (рис. 11.36, а), самодуальным. Нормированные величины волновых сопротивлений ступеней линий схемы рис. 11.38 составляют

Wa = hW26 = 0,87635. Wa = = 0.74772.

При значениях п = p/q н р 4 предпочтительны численные методы отыскания величин волновых параметров ступеней линий.

Допустимы и другие конструкции, например полосковая, обеспечивающие в данном варианте расчета пренебрежимо малые связи между проводниками 1 и 2.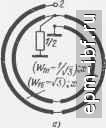

Рис. 11.36. Схема ТЛ 1 : 2 (а), эквивалентная цепь (б) и внешний вид ТЛ (в)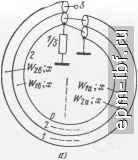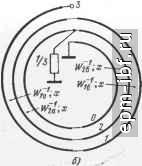

Рис. 11.37. Варианты выполнения ТЛ 1 :3 коаксиальный (а) и дуальный ему полосковый (б)

Так, например, при /г = 4 для варианта рис. 11.39, а* численный расчет дает

= 0,302, Г1б = 0,885, W = 1,57, \W6 = 2,955, Гза = 3,59, W = 3,873. Одним из путей получения больших значений п служит кас-2/5 кадное соединение составляющих ТЛ

с последующим объединением проводников, имеющих эквипотенциальные зажимы, и образованием единого устройства. Примером служит ТЛ 1 : 4 (рис. 11.39,6), составленный из двух ТЛ 1 : 2 типа ТЛ, показанного на рис. 11.36, а.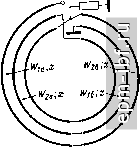

* Аналогичным образом строятся схемы и для больших значений п.

Рис. 11.38. Вариант выполнения ТЛ 1 :3/2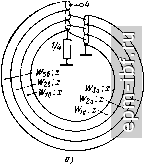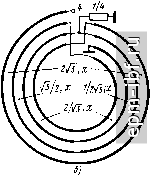

Рис. 11.39. Варианты выполнения ТЛ 1 : 4

а - коаксиальный; б - полосковый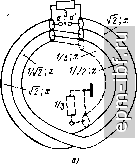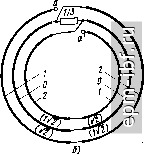

Рис. 11.40. Варианты выполнения ТЛ ±(1:3) 210

ТЛ ± (/ : п). Помимо хорошо известного ТЛ ± (1 : 2), на двух линиях простейшими являются ТЛ ± (1 : 3/2), рассмотренный в § 11.6, и ТЛ ± (1 : 3) - на рис. 11.40, а. Общий случай такого ТЛ ± (1 : 3), изображенного на рис. 11.40, б, при связях между всеми проводниками в каждой из двух идентичных ступенях характеризуется матрицей волновых проводимостей [Glgxa элементами Оц = a/k, Gi = l/k, G = (2a + l)lk, где k = = V {a+ l)(2a- 1).

Из условий физической реализуемости матрицы [G] имеем 1 < а< оо. При этом tg (гр/2) = (1/2) (а + ХУ (2а - 1)-/ tg х. Крайним значениям а = 1 и а = оо отвечают соответственно схемы рис. 11.40, а и б с величинами волновых сопротивлений, указанных в скобках. Любая из этих схем может быть выполнена в коаксиальном или полосковом варианте.

Более сложным является ТЛ ± (1 : 4), выполненный, в частности, по дуальным схемам (рис. 11.41, а, б)*. Аналогичным по сложности и характеру связей между проводниками является ТЛ ± (2:4), выполненный согласно схеме рис. 11.42. Ему может быть отдано предпочтение перед хорошо известным ТЛ ± (1 : 2) на двух линиях, ввиду возможности реализовать большую шунтирующую индуктивность при равном габарите. Заметим, что в линиях этого ТЛ, как и в согласованных ТЛ + [1 : (Л^ + 1)/Л^] из § 11.6, имеет место режим бегущей волны.

Симжтрирующие ТЛ. Такие ТЛ типа 1 : ±/г/2 при п> 1 можно получить из симметричных путем введения дополнительной симметрирующей линии, как это показано штриховой линией на рис. 11.40, а.

Неповышающие ТЛ п : ±1/2 при /г 1 рационально строить из ТЛ I : п с дополнительной симметрирующей линией, один проводник которой совмещен с проводником ТЛ 1 : п. Примером служит ТЛ 2 : ±1/2 (рис. 11.43), в котором с помощью дополнительного проводника, введенного в ТЛ 1 : 2, осуществляется симметрирование на понижающей стороне.

Гальванически развязанные ТЛ ± (1 : п) могут быть получены на основе схемы типа рис. 11.8. Для простейшего из них ТЛ ±(1:2) в общем случае (рис. 11.44, а) элементы матрицы волновых проводимостей каждой из двух идентичных ступеней трехпроводной линии составляют G = 2aJk, G12 = 2/k, G22 = 2 (За + + 2)/k, где k = Y {а+ 1) (За - 1), причем 1 < а < оо. Для этого ТЛ tg (i)/2)= (а+1)2 (За-1)-1/2 tgx. В скобках приведены величины волновых сопротивлений для а = 1 (в линиях бегущая волна).

При других значениях п, в частности /г = 3 и /г = 4, справедливы, например, схемы рис. 11.44, бив соответственно.

Различные симметричные ТЛ можно включать каскадно, а затем объединять проводники, имеющие общие зажимы. Так, напри-

* Для всех ТЛ ± (I : п) обе ступени многопроводной линии идентичны.

мер, соединив гальванически связанный ТЛ ± (1 : 3) и гальванически развязанный ТЛ ± (1 : 2), получим гальванически развязанный ТЛ ± (1 : 3/2), один из возможных вариантов которого приведен на рис. 11.45. Для него

tg (ф/2) = ((21/2 + V3J tg х\ (2Кб ~ tg х]-К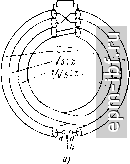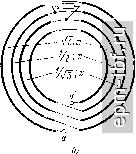

Рис. 11.41. Варианты выполнения ТЛ ±(1 :4): а - коаксиальный: б - полосковый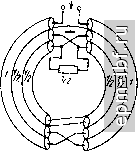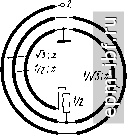

Рис. 11.42. Вариант выполнения ТЛ ±(2:4)

Рис. 11.43. Простейший понижающий симметрирующий ТЛ 2: ±1/2

Заключительные замечания. Из изложенного в настоящем параграфе видно, что основой для различных ТЛ с предельно широкой рабочей полосой частот служат ТЛ 1 : я и ТЛ ± (1 : п), выполненные из двухступенчатой многопроводной линии. Общий случай ТЛ 1 : п при п = {т + \)lk (рис. 11.46) описывается с помощью матрицы передачи, связывающей переменные на входе и выходе {т + 1)-про-водной линии:

cosa: /[Gi]-i sin;c j г [1] cos;c / [Gj] -1 sin jc

/ tGiJxm sin * nimxm os X \ [j [Glm

(11.28)

где [Ux] = [U{\ U\ и<,Ц', (/il = [/l, /( ] и анало-

гично для [t/j] и i/al; [GJ и [Gal - матрицы волновых проводимостей ступеней линии; [1] - единичная матрица.

z о (II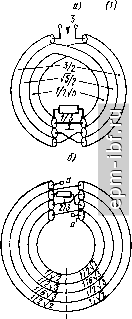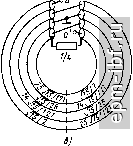

Рис. 11.44. Гальванически развязанные ТЛ:

а - общий случай ТЛ ±(1:2); б - тл ±(1 : 3) иа коаксиальных линиях; в - ТЛ ±(1:4) на коаксиальных линиях

Рис. 1.45. Вариант выполнения гальванически развязанного ТЛ ±(1:3/2) на коаксиальных линиях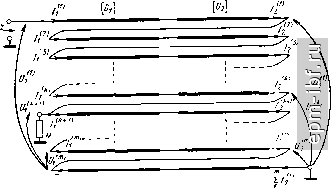

Рис. 11.46. Общий случай схемы ТЛ 1 : га