магнитопроводе III, а линии в схеме, подключенной к зажимам 2-5, - на магнитопроводе II. Таким образом, устройство в целом выполнимо на трех магнитопроводах без использования линейных комбннацпй продольных напряжений.

Область нижних частот. При любом из указанных вариантов реализации двух последних столбцов матрицы (2.42) анализ параллельно соединенных схем рис. 13.12, а, б дает

MR О

О О

о

(l ?)+l o)Li l (oLi О

[П4 =

О

1 o)Li

(] ?) + l o)(LiL2) О

О О

о

(1 ?) + 1 со1з.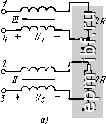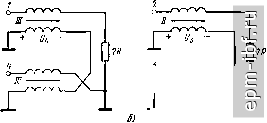

Рис. 13.11. Варианты схем (а, б), реализующие третий и четвертый столбцы матрицы (2.42)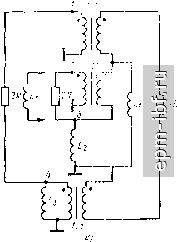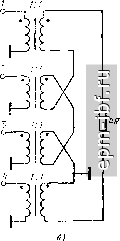

Рис. 13.12. Схемы замещения для цепей рис. 13.G, я в области нижних частот

(шуНТН])уЮ1Ц11е ПИДУКТНННОСП! 0ТНСССП1,1 к ЦСМП1 ТИ11.-1 I IHI рнс, 13.(), а)

Если подключить дополнительную индуктивность Ly между зажимами 2 и 5, то будет полная развязка между входами 2 и 5, в этом случае

J- М 1 . 2 1 , 1 1,1

[FU = ciiag-

R jcu(L2Z.i/2) R jouLs

Область верхних частот. Будем считать, что электрические длины всех отрезков линий (возможно, кроме дополнительных) одинаковы и равны X. Тогда при реализации двух последних столбцов матрицы (2.42) сопротивлениями 2R или схемами рис. 13.11, а достигается полная развязка между любым из входов одной пары (1, 4) и любым из входов другой пары (2, 3), вне зависимости от величины волнового сопротивления W, одинакового для всех основных линий. Дополнительные линии предполагаются согласованными. Величину волнового сопротивления основных линий следует выбирать из условия наилучшего согласования (единого для всех входов) при равноамплитудных источниках, относительные фазы которь(х соответствуют первому или второму столбцам матрицы (2.42). Для каждого из этих случаев минимальное рассогласование имеет место при W = Y2R и определяется из (12.10). Рассчитывая величину развязки между входами в парах (/, 4) и (2, 3) с помощью матрицы собственных векторов (2.30) при k = 2, находим, что при W ~Y2 R li, = I23 = 10 lg2{[(4 + igHfligHl + 2} [дБ].

При использовании схем рис. 13.11, б также сохраняется полная развязка между любым из входов пары (/, 4) и пары (2, 3), а между входами в парах (/, 4) и (2, 3) она становится большей, но увеличивается рассогласование. Если длины линий схем рис. 13.11, б и их волновые сопротивления принять теми же, что и схем на рис. 13.6, а, то наименьшее рассогласование будет при W = YR; оно находится из (13.1).

13.4. УСТРОЙСТВА ПОПАРНОГО СЛОЖЕНИЯ МОЩНОСТИ

Широко распространены устройства попарного (двоичного) соединения простых составляющих, отвечающие матрице (2.44). В качестве этих составляющих применимы устройства, которые рассматривались в § 12.2 и 12.3. Можно, например, получить устройства, отвечающие матрице (2.42), если исключить на рис. 13.7, а схему III, заменив ее в простейшем случае двумя сопротивлениями RI2, подключенными к освободившимся зажимам схем I и II.

Если требуется сохранить полную развязку между входами 1-4 в области верхних частот, существующую в схеме рис. 13.7, а, то вместо этих сопротивлений RI2 следует подключить цепи рис. 13.13, а. Аналогичным образом можно исключить схему III на рис. 13.9. При этом допустимы два магнитопровода, а для сохранения полной развязки между входами 1-4 в области верхних частот следует заменить сопротивления RI2 на цени (рис. 13.13, б).

Рассмотрим Теперь двоичные устройства с использованием схем рис. 12.9, а, обеспечивающие повышающую трансформацию. Простейший случай (рис. 13.14) отвечает матрице (2.42).

Область нижних частот характеризуется матрицей

1 1 .

R /o)(L,jL,)

= W + [[П^+(1 2) [1Ы, (13.4)

где IF]/* = [Y] есть диагональная матрица проводимостей для входов / и 2 схемы рис. 12.9, а. В (13.4) и далее символы+, ll.lUa.z означают соответственно прямую сумму матриц [61 ], параллельное соединение индуктивностей и матрицу второго (в общем случае п-го) порядка, состоящую только из элементов +1.

Рис. 13.13. Цепи, заменяющие исключенную схему III: о -на рнс. 13.7, а; б - иа рнс. 13.9, а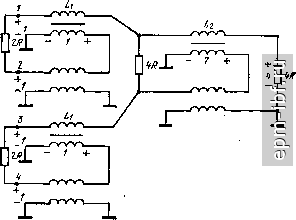

Рис. 13.14. Двухступенчатое соединение простых устройств 252

Из (13.4) нетрудно видеть, что при подключении индуктивного элемента между зажимами 3 и 4 матрица [Klj становится диагональной:

[Y]<d) = [YY/) + [[у](/) + (2 coLa) UJ. (13.5)

Область верхних частот. Устройство здесь согласовано как в режиме деления мощности, так и при сложении мощностей равноамплитудных синфазных источников на входах 1-.Ълагодаря симметрии схемы (рис. 13.14) развязка между входами /-2 та же, что и между входами 3-4, т. е. = ?34 = li- Кроме того, lis = ?2з = = 1и = ?24 = 2 =5 li- Расчет этих величин приводится ниже для общего случая k ступеней.

Рассмотрим теперь трехступенчатое соединение таких же схем. Для области нижних частот (рис. 13.15, а) матрица проводимостей, записанная относительно входов 1-8, имеет вид

IY], = IY],+ [[Yl + (I C0L3) [1)4,41,

(13.6)

где [К]4 определено в (13.4). Подключив в первой ступени между зажимами 3-4 и между зажимами 7-8 индуктивные элементы L, а между зажимами 5-8 полный четырехугольник из индуктивностей La (или эквивалентную ему звезду из индуктивностей L3/4), получим

[YY/) = [Y][) + [[У](/) + (4 C0L3) [П4.41, (13.7)

где [У]/) определено в (13.5).

В режиме деления мощности коэффициент отражения со стороны несимметричного относительно земли резистора 8R

5 = 2 2 [l/{8Ryi+\)]-l, /= 1

(13.8)

где г/г - проводимость параллельного соединения сопротивления величиной 8R/7 и индуктивности i-ro диагонального элемента матрицы (13.6).

Для области верхних частот матрицы IS], [Z] и IY] схемы (рис. 13.15, б) имеют собственные векторы, выражаемые столбцами матрицы (2.30) при k = 3. Этим векторам соответствуют четыре различные функции (собственные значения матриц): Zj, Zi, Z2 и Za, необходимые и достаточные для получения элементов матрицы рассеяния трехступенчатого соединения. Функция Z (рис. 13.15, в) отвечает первому столбцу матрицы (2.30), т. е. рабочему режиму, а функции Zi - Z3 (рис. 13.15, г) соответственно при v = 1, 2 и 3 отвечают остальным ее столбцам.

Рассмотрим теперь общий случай k ступеней.

Область нижних частот. Здесь, если полагать, что Fi = \/R, справедлива следующая рекуррентная формула:

[7]2А = [У]2*-1 + {[П2*-1 +(l coLft)[l]2*-i, 2*-}- (13.9)

Из нее, в частности, следуют (13,4) и (13.6),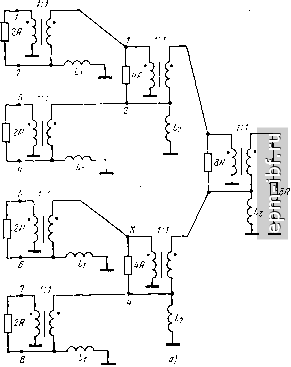

При подключении развязывающих индуктивных элементов, дна-гонализнрующих матрицу (13.9),

Столбцы

VVV\ \\V\\

1 ступень i Z отупень

I I I 1 I I i 1 ffUX-X I

I I I I I I I 1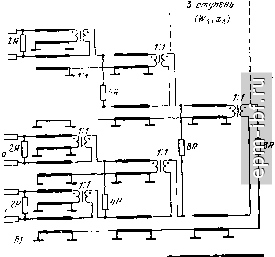

[Y\\V = [Yty-x + i[Fl*2l*-,+(2*- ;,)[ll2*-i, 2*-il. (13.10)

если полагать, что Y) = 1 ?. Из (13.10) следуют (13.5) и (13.7).

Нетрудно видеть, что начиная с трех ступеней резко возрастает количество развязывающих индуктивностей. Они подключаются полными многоугольниками (или эквивалентными звездами ), приводящими к нулю все внедиагональные элементы матрицы (13.9), которые в свою очередь добавляются к диагональным, образуя (13.10).

Количество развязывающих индуктивностей можно уменьшить и сделать минимальным, если их подключать не только на входах первой ступени (в значительно меньшем количестве), а еще и на входах последующих ступеней, начиная с предпоследней, обеспечивая там развязку. Развязывающие индуктивные элементы устанавливаются только между входами индивидуальных схем рис. 12.9, а. Так, например, при трех ступенях (рис. 13.15, а) в первой требуются индуктивности между 3-м и 4-м зажимами, L3/2 между 5-м и 6-м и L2 II Z.3/2 между 7-м и 8-м, а во второй - индуктивность между 3-м и 4-м ее зажимами.

В режиме деления мощности коэффициент отражения на (2* --1)-м входе определится как

5 = 2 2 П/(2*/?У, + 1)1-1,

где Hi - проводимость параллельного соединения резистора 2R/{2 - 1) и индуктивного элемента, соответствующего i-му члену диагональной матрицы (13.10).

Область верхних частот. При произвольном числе ступеней (к) матрицы [5], [Z] и IY] относительно входов 1-2 имеют систему собственных векторов, являющуюся столбцами матрицы (2.30). Этим столбцам отвечают собственные значения, определяемые, как было показано выше, простыми схемами. Найдя их входные сопротивления (или проводимости) и используя принцип суперпозиции, можно составить выражения общего вида для элементов матрицы [S1.

Первому (синфазному) собственному вектору, т. е. рабочему режиму, отвечает собственное значение Zq/W = 1 (рис. 13.15, в). Для второго, четвертого, шестого и остальных собственных векторов четного порядка все ступени, начиная со второй (к == 2), можно считать отключенными, поскольку на вторую ступень колебания не поступают. При этом на всех развязывающих резисторах первой ступени имеются равные напряжения, симметричные

Рис. 13.15. Схема замещения трехступенчатой системы для области нижних частот (а), верхних (б) н цепи, определяющие собственные значения ее матрицы рассеяния {в, г)