Область нижних частот. В силу сказанного выше, в рабочем режиме все входы не шунтированы индуктивностями и поэтому осуществимо согласование. Развязка между входами идентична для обоих вариантов включения развязывающих резисторов R и рассчитывается с помощью собственных векторов, составляющих столбцы матрицы (2.31). При воздействии только первого собственного вектора (\/УЛ)[\, 1, И' не учитываются резисторы R и все индуктивности намагничивания L. Собственное значение, соответствующее этому вектору, есть сопротивление R, согласованное с источником. Каждому v-му из остальных {N - 1) собственных векторов соответствует собственное значение, определяемое цепью из параллельного соединения сопротивления R и действующей индуктивности Lv, определяемой уравнением:

Uexp [/2я (V - 1) (г - \)/N] = = /со1/ (2 ехр [/2jt (v 1) {i - \)/N] - - ехр [/2я (V - 1) {i - 2)/т - ехр [/2лг (v - l)/N]}, .

где V = 2, 3, N; (i - 2)ji = N; U - амплитуда напряжения на каждом входе; / - амплитуда тока.

Разложив два последних члена (вектора) в правой части этого уравнения на составляющие, синфазные первому вектору и перпендикулярные ему (противофазные друг другу), нетрудно получить, что

= 2L [1 - cos (v - 1) (2n/N]], (14.8)

причем = л^+2-г*

Суммируя токи на каждом входе, нагруженном на сопротивление R, от компонентов всех собственных векторов, получим

J у + / у fn -, na-- i)/N 2 R+}2coL

Векторы напряжений на равных элементах (14.8) симметричны относительно вектора е- . Представив суммы этих симметричных векторов в виде синфазных (совпадающих с е- ) и противофазных (в сумме равных нулю) составляющих, получим

для четных N и

L+ + + cos (,--!) я -f 2 У В.

2 +2/0)1(/2+., v-Tz

/£ =

+2 2

v = 2

(14.9)

(14.10)

Для нечетных N. При этом

R + j(oL

(v-l)(l-l)

Подставив в (14.9) и (14.10) значения из (14.8), получим

l + iig \

-+7S87<°(-) +2lv

v = 2

при четных N и

(N+l)/2

+ 2 2

v= 2

при нечетных, где g = aL/R, а

+2g[l -cos 2л(у-1)/JV1

1 +4g [1 - cos 2л (v- l)/N\

cos [2л (v~l)(i-{)/N].

Зная результирующие токи, определим элементы матрицы рассеяния из соотношении

Sii=--{2IiR/E)-\ (1 = 1,2,3, ...,N), Su = 2IiRlE (i = 2,3, ...,N) и соотвественно lu [дБ] = -201g Si; ti.

(14.11)

Ввиду наличия поворотной симметрии схемы развязка между любыми двумя равноотстоящими друг от друга входами одна и та же (см. § 2.3), т. е.

Si, i+k = S,-, если j> k, и i+k = Sj (n~j+h)> если / < k. Простой расчет с помощью вышеприведенных выражений дает: для = 3

Su = 2/3(1 + /6g), = Sj3 = 53 = -1/3(1 + /6g);

для N = 4 Su = (3 + /20g)/4 (1 + /12g - 32g2),

512 = Su = S23 = S34 = -1/4 (1 + j8g),

513 = 54 = -(1 + / 12g)/4 (1 + /12g - 32g2); для N = 5

Su = (4 + /20g)/5(l + j\Og - 20g),

512 = = S23 = S34 = S45 = -1/5 (1 + j\Og - 20g%

513 = = S = =. S35 = -(1 + /10g)/5(l + j\0g-20g). При выборе магнитопроводов необходимо знать, помимо зависимостей I = / (л;), еще и продольные напряжения {Ui), возникающие в аварийных режимах, в частности при коротких замыканиях на входах. Определим их, полагая сначала, что первый вход корот-козамкнут, а на всех остальных (г = 2, 3, N) имеются равные напряжения U. Этот режим можно представить как суперпозицию двух режимов:

а) на каждом входе действует напряжение U; при этом все продольные напряжения равны нулю, а t/arp = U;

б) на первом входе напряжение равно -U, а остальные входы короткозамкнуты. При этом t/нагр = -U/N создается только первым собственным вектором, для которого все продольные напряжения равны нулю. Результирующее напряжение на нагрузке составит

(Л^ - 1) UIN, и оно равно удвоенному значению продольного напряжения Ui = Un, поскольку 1 = In. Остальные продольные напряжения, меньшие чем {N - 1) III2N, просто находятся по закону Кирхгофа.

Таким образом, наибольшее продольное напряжение t/imax> возникающее при коротком замыкании одного входа, составляет {N - 1) U/2N. Методом суперпозиции можно определить также напряжения на обмотках при коротком замыкании нескольких (т.) входов. В этом случае напряжение на нагрузке составит

{N - т) U/N, а Ui ах = т {N - т) U/2N.

Область верхних частот. Используем тот же метод собственных значений применительно к схеме замещения, образовав ее из рис. 14.16 заменой каждого ЭТЛ схемой рис. 10.5, б.

Если развязывающие резисторы R соединены Л/-лучевой звездой между входами, как это было упомянуто выше, то

Su =

й -/2 ctg л; 1-/26 cte,x \

6 -;2ctg 1-;26ctgj:

Qi = ioig-

a развязка между входами = 20 Ig + Qi, где b = W/R;

(1 +16 ctg* x)+A(\ +6) ctg- X A[b + {\+bfcigx]

Рабочий коэффициент отражения на каждом входе составит

Tl = 5+ = Ь/ф - /2ctg л:). (14.12)

Если развязывающие резисторы соединить, как показано на рис. 14.16, то развязка увеличивается. При W = R элементы матрицы рассеяния, определяемые тем же методом, что и ранее, составят 8ц = Sift = 1/Л^(1 - /2ctg л;). Соответственно = Q2 + + 20 Ig N, где Q2 = 10 Ig (1 + 4 cigx) то же, что и для схемы рис. 14.5, а коэффициент отражения на каждом входе в рабочем режиме (Га) определится из (14.12) при b = \.

Используя (2.36), где следует принять S = О, а S+ согласно (14.12), получаем

S 3 = {M/N)/{2 - {M/N) - /2ctg л:],

Sy, = {M/N)/{M/N - j2cigx).

Достижимо расширение полосы схемы рис. 14.16 за счет подключения к общей нагрузке разомкнутой на конце линии с волновым сопротивлением R/l\/ и электрической длиной х. В этом случае

= 5. = l/N{l - 2ctg2A: - /2ctgA;). Развязка между входами ?з = Qs + 20 Ig Л^, где Qa = 10 Ig (1 + 4 ctgx), а рабочий коэффи-

циент отражения на каждом входе Г3 = S+ = 1/(1 - 2 ctgjc-/ ctg х). Подставив S+ и S- = О в (2.36), найдем зависимости S и S.

Дальнейшее расширение полосы осуществляется при подключении к каждому входу разомкнутой на конце линии (R/q; х), а к нагрузке - разомкнутой на конце линии (R/Nq; х). При этом

Y S+ = {l~2q+q4gx) tgx

* (-q4gx + 2q+l)tgx-i2(l-qtgx)

S- = [-1 + {j2/q) Ctg x]-\ h = Qi + 20 Ig N,

rfleQ4 = -20 1gS+-S-.

Ha рис. 14.17 иллюстрируется эффект расширения полосы при усложнении коррекции и возможность получения чебышевской зависимости при надлежащем выборе величины q.

Можно воспользоваться также сосредоточенными корректирующими элементами, в частности результатами расчета для устройств рис. 12.9, а и 14.5. В рассматриваемом случае должна использоваться дуальная цепь коррекции, устанавливаемая со стороны общей нагрузки R. При нормировании к величине волнового сопротивления каждой линии, деленной на N, упомянутые применительно к рис. 12.10, б, в величины bi заменяются на Ьа (и наоборот), а R - на R- и тогда рабочий коэффициент отражения определяется непосредственно по рис. 12.10, б, в, а величина развязки - выражением I = 20 Ig /V + Q.

Осуществимо также устройство параллельного типа с полным согласованием и высокой развязкой в области верхних частот. Рассмотрим схему (рис. 14.18), полученную из исходной (рис. 14.4) заменой всех Тр 1 : 1 идентичными ЭТЛ и подключением дополнительных фазокомпенсирующих линий.

И

0,11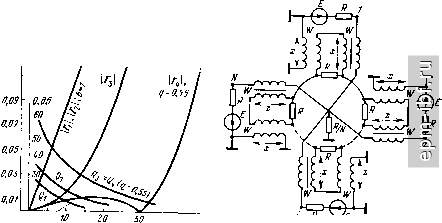

Рис. 14.17. Расчетные зависимости Q = f(x) и Г|=/(д:) для устройства, приведенного на рис. 14.16

Рис. 14.18. Согласованное устройство параллельного типа

Область нижних частот. При равноамплитудных синфазных источниках на всех входах обмотки всех Тр, к которым подключены развязывающие резисторы R, оказываются закороченными (см. § 14.1). Это означает, что все источники согласованы. Развязку между входами определим, как и для схемы рис. 14.16, с помощью собственных векторов.составляющих столбцы матрицы (2.31).

Для первого (синфазного) собственного вектора соответствующее собственное значение определится согласованной для каждого источника цепью. Для каждого из остальных собственных векторов общая нагрузка RIN имеет нулевой потенциал, и поэтому ее можно считать закороченной. Поскольку сумма продольных напряжений на всех обмотках, соединенных последовательно, равна нулю, то проводники, соединяющие эти обмотки, можно считать разомкнутыми, ибо по ним не течет ток. Поэтому собственное значение, соответствующее каждому из упомянутых собственных векторов, определяется цепью, состоящей из соединенных параллельно развязывающего сопротивления и шунтирующей индуктивности L трансформатора.

Полагая, что источник {Е; R) подключен к любому одному (пусть первому) входу, и суммируя токи в сопротивлениях R на каждом входе от воздействия компонентов собственных векторов, получаем, что ток на входе /, где подключен источник, Д = {E/2NR) [1 + -Ь 2 (я - 1) (1 4- lb)/(l + /26)], а ток в сопротивлении на каждом из остальных входов Iii = -E/2nR (1 -}- /26), где b = aL/R. В соответствии с (14.11) элементы матрицы рассеяния 8ц = = {2IiR/E)-I = (N(I + j2b), Sik =2 ,7?/£ =

= - 1/Л^ (1 4-/26)*, а развязка между входами g [дБ] = = -20 Ig ] Sjft I = 20 Ig + 10 Ig (1 + 46). Ее можно увеличить, если последовательно с каждым из развязывающих резисторов R подключить конденсатор С, образующий вместе с L фильтр верхних частот и не влияющий на согласование в рабочем режиме [98].

Определим теперь наибольшие продольные напряжения в аварийном режиме замыкания т входов из N, считая, что на оставшихся имеются равные напряжения Е. При этом будем пренебрегать шунтирующим действием индуктивностей намагничивания.

Предположим, что напряжение U имеется лишь на одном, пусть первом входе, а все остальные входы короткозамкнуты. В этом случае получаем схему рис. 14.19. Полагая теперь, что напряжение U имеется на любом другом входе, и используя принцип суперпозиции, нетрудно получить, что наибольшее продольное напряжение

Umax

mU/N, если т > N/2

(N-m) и IN, если mN/2

* Полагая в (2.36) S+ = О, а S- = = {M/N-\)/ll ,Т, (M/N) + j2b].

- (1 -f j2b)-\ имеем 53,=

Г

При этом напряжение на общей нагрузке составит Ua = {N - - т) Vim.

Область верхних частот. Схема замещения устройства образуется из рис. 14.18 прн замене каждой линии, связанной с магнитопроводом согласно рнс. 10.5, б. При анализе этой схемы используем тот же метод собственных векторов-столбцов матрицы (2.31). Для первого (синфазного) собственного вектора развязывающие резисторы, соединенные последовательно в кольцо, можно считать коротко-замкнутыми (поскольку напряжение на каждом из них равно нулю), и цепь, определяющая собственное значение, является согласованной. Для каждого из остальных собственных векторов потенциал на общей нагрузке равен нулю и ее можно считать коротко замкнутой.

Используя симметрию получаемой при этом схемы, разделяем ее на простые составляющие цепи в соответствии с холостым ходом по осям нулевого тока и коротким замыканием по осям нулевого потенциала. Затем, с помощью принципа суперпозиции и несложного, но относительно длительного расчета, получим, что для N =3 = Егз = liz = lOlg 9 (1 + 36 zigx); для N=4

а = 24 = 10 Ig 4 (1 + 4 ctgx).

=14 -

=2 3

He нарушая согласования в рабочем режиме, можно, в частности, для ЛГ = 3 существенно увеличить развязку между входами, если последовательно с каждым из резисторов с сопротивлением R включить короткозамкнутую на конце линию с волновым сопротивлением .R/3 и электрической длиной х. В этом случае gig = 2 3= 1з1= 10 Ig [9(1 + 324 ctg*x)].

Все характеристики рассматриваемого устройства останутся неизменными, если выполнить его с симметричными относительно земли входами и общей нагрузкой (рис. 14.20), что является обобщением устройства рис. 12.16.

В заключение отметим, что, помимо устройств, рассмотренных выше, существует еще целый ряд других, в частности, устройства параллельного типа, анализ которых выходит за пределы настоящей книги.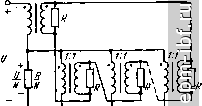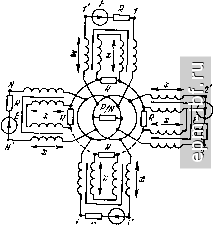

-Г77Т77777ТГ7ТГТ7777Т7Т77777777 £

Рис. 14.19. Вспомогательная схема для определения {/пр max

Рис. 14.20. Согласованное устройство параллельного типа с симметричными

входами