2.2. СОГЛАСОВАНИЕ И РАЗВЯЗКА В МОСТОВОЛ\ ВОСЬМИПОЛЮСНИКЕ

При анализе устройств, содержащих минимальное число развязывающих резисторов (§ 1.5), удобно относить их и нагрузки к внешним зажимам и рассматривать устройство как цепь без потерь.

Между условиями согласования и развязки такого мостового восьмиполюсника имеется взаимосвязь, аналитически вытекающая из унитарности матрицы рассеяния и выражаемая нижеследующими тремя основными свойствами. Свойство 1.

Если у восьмиполюсника {4Р-цепи) без потерь все входы согласованы, то они попарно развязаны. Согласование на всех входах выражается равенством нулю всех элементов главной диагонали матрицы (2.4), т. е. 5ц = S = S33 = S44 = 0. Раскрывая условие унитарности матрицы [S], выражаемое соотношением (2.6), и учитывая равенство нулю ее диагональных элементов, имеем:

[S]*[S] =

иначе

= [1)4.

(2.9)

где подматрицами обозначено:

[1,1] =

Sl3 23 +S,4S,

14-24

23 13 5

[1,2] =

[2,1] =

24 -14 12 23 + S34 l Sl2 + S24 S34

S23 + 5з4 8ц 24 11 + S34

[2,2] =

5i3+S23p + S342

14 13 ~Ь Spi S>

24 -23

I512P+IS23P+IS2J S12 524 -- Si3 S34 12 + 23 3>,

13 Si2 + 534 5-24 14 S12 + S34 S23

13 + 23 S24 Sk+S24P + S34N

Из сопоставления полученной матрицы с единичной следует, что ее диагональные элементы (1,1), (2,2), (3,3) и (4,4) равны единице,

а остальные - нулю. Складывал элемент (1,1) с (2,2) и вычитая элементы (3,3) и (4,4), получаем

= \SJ\ (2.10)

12

Складывая элемент (1,1) с (3,3) и вычитая (2,2) и (4,4), получаем

12

= IS,

24 1

(2.11)

Складывая, наконец, (1,1) с (4,4) и вычитая элементы (2,2) и (3,3), получаем

Si4r=S23r. (2.12)

Из сопоставления элементов (1,2), (1,3) и (1,4) с нулевыми имеем

Sl3 S23 - Si4 S24, S12 S23 - Si4 S3

S12 Si3 - S24 S34.

Перемножив левые и правые части этих трех выражении, найдем

(Si2Si3S2 3) = - (Si4S24S34).

Это соотношение справедливо с учетом (2.10)-(2.12) только при условии, что S12S13S23 = S14S24S34 = О, т. е. по меньшей мере один элемент в каждом произведении равен нулю. При соответствующей нумерации входов всегда можно считать, что S12 = 0. Тогда согласно (2.10) S34 = 0. В результате матрица 4 Р-цепи примет вид

[S] =

или в сокращенной записи

[S] =

[0]2

[S][

[0]2

(2.13)

(2.14)

где [S]i =

- унитарная матрица (подматрица); [0]2-нуле-

вая матрица второго порядка. В частности, для устройств на идеальных трансформаторах матрица [S] вещественная и, следовательно, ортогональная, т. е. [S]i = [S]r\ Свойство 2.

Если у восьмиполюсной цепи без потерь два входа согласованы и развязаны, то два других входа также согласованы и развязаны. Пусть согласованы и развязаны входы 1 и 2. Тогда матрица рассеяния имеет исходный вид

[Sl=-

[0]2

[S]i

[S]i [S]ii

(2.15)

Условие унитарности матрицы можно записать как IS] [S]* =

откуда непосредственно следует, что

[S]i[S]\ = [11 [S],[5] = [OU. (2.16)

Из (2.16) следует, что матрица IS]] невырожденная. В этом случае второе соотношение возможно, только если [Sin = [Ola, что и доказывает свойство 2.

Найдем соотношения между элементами матрицы (2.13) согласованной восьми полюсной цепи с попарно развязанными входами. Эти соотношения, в частности, понадобятся при рассмотрении свойства 3.

Отношение Sig/Si * = m есть коэффициент деления мощности устройства при подключении источника ко входу 1. Из (2.11) и (2.12) следует, что

52з/5а4= 1/т. (2.17)

Можно также определить и модули элементов подматрицы [SJi, входящей в (2.14) используя ее унитарность, означающую, что

I Si3 Г +1 Su\ 1, I S231 +1 Г= 1, §13523 +SuS - 0. (2.18)

Решая совместно (2.17) и (2.18), получаем

Si3l=S24=l n+l)=/, I Si4= I S23I = = /Т^.

(2.19)

В случае равного деления мощности (т = 1) имеем S131 = 1S141 = = 1/]/ 2.

Определим теперь возможные соотношения между аргументами элементов матрицы [Sli, входящей в (2.14). Пусть

Si3=/ ехр /cpi3, S14 = Yl -2 ехр ;cp , S24= t ехр /Ф24, S23 =yi-t ехр Подставив эти выражения в (2.18), получаем

(Ф1з - Фи) = (Фаз - Ф24) - я. (2.20)

Следовательно, подключенные ко входам 1 п 2 источники могут создавать на нагрузках, подключенных ко входам 3 или 4, равные по амплитуде колебания, разность фаз которых различается на 180°. Это свойство согласованной 4Р-цепи в сущности определяет возможность сложения мощностей без потерь. Рассмотрим некоторые случаи.

Пусть Ф13 = Фи = Ф24 = о, тогда фаз = я. Матрица рассеяния такой цепи

[S] =

О

о

-у\~[ о о

/-]гг72 t о о .

(2.21)

описывает схемы, в которых сигнал со входа / делится между входами 3 vi 4 синфазно, а сигнал со входа 2 - противофазно. Такая матрица описывает класс синфазных или синфазно-противо-фазных устройств.

Для квадратурных устройств Ф13 = Фа4 = О, а Ф14 = я/2. Из (2.20) следует, что фаз = я/2. Соответственно S13/S14 =

= -jVm, S23/S24. = }/Vm

t jVT

/КГ=Я t о О

о о

[S] =

о о

о о

(2.22)

Возможны, наконец, синфазно-квадратурные устройства, для котх)рых ф1з = О, Ф14 = Фа4 = я/2. Из (2.20) находим, что фаз = = я. Следовательно,

[51 =

О О

- /Т-F it

о о

и в этом случае S13/S14 = -jYTn, а 52з/5а4 = j/Vm.

Свойство 3.

При наличии симметрии и развязки между двумя входами восьми-полюсная цепь без потерь согласована по всем входам [131. Здесь имеются в виду устройства, обладающие одним из следующих типов симметрии (рис. 2.3):

а) симметрия относительно вертикальной оси б - б, при которой

it о

о

(2.23)

--г

Sii - S33, Saa - S44, Si4=Sa3, Sia= S34, (2.24a)

Рис. 2.3. Общий вид симметричной 4Р-цепи

б) симметрия относительно горизонтальной оси а - а, при которой

Sxi = 44, 5зз = 5221 ~ 524, 52 = 5з4, (2.246)

в) полная симметрия, т. е. относительно осей а-а и б - б при 5и = 522 ~ 5зз = 544, 52 = 5з4, = 524, 5i4 = 523- (2.24 в)

Иными словами, при наличии симметрии достаточна лишь развязка между двумя входами для того, чтобы восьмиполюсная цепь без потерь имела матрицу рассеяния (2.13).

Для каждого типа симметрии это свойство вытекает непосредственно из условия унитарности. Так, например, полагая для случая симметрии относительно оси а - а, что 5i2 = 5з4 = О, и подставляя это условие в развернутые соотношения (2.9), получаем, в частности,

5и 5i3 + 5i3 5u = I 5u 115i31 cos (Фц- Ф13) = 0.

522 524 + .524 §22 = 522 j 524 I COS (Ф22- Ф24) = 0

Очевидно, что по меньшей мере един из сомножителей в каждом из этих соотношений тождественно равен нулю. Нулю не могут равняться ни 5i3, ни 524, так как в любом из этих случаев в совокупности с 5i2 = 5з4 = О устройство превращается в две раздельные 2Р-цепи. Очевидным контрпримером, когда cos (Фц - Фи) =5 О и cos (Ф22-Фз4)=70, являются схемы на идеальных трансформаторах, поскольку для них фгь = О или я. В результате оказывается, что 5x1 = 522 = О и, в соответствии со вторым свойством, 5зз = = 544 = О, т. е. 4Р-цепь характеризуется матрицей (2.13). Ана-логичнымбразом доказывается свойство 3 во всех остальных случаях.

В зависимости от типа симметрии и соответствующего выбора развязанных входов, разность аргументов внедиагональных элементов может составить лишь О, я или л/2 (она может быть дополнена целым числом периодов). Так, например, при полной симметрии, когда коэффициенты рассеяния равны не только по модулю, но и по фазе (S13 = 524 = Р, а 5 = S23 = v),

О О р Y

О О Y р

р V О О

7 р О 0

[5] =

(2.25)

В силу унитарности этой матрицы

lv2 + p[2 - 1, а yP + PV О,

(2.2Й)

откуда следует, что угол сдвига между Р и у составляет 9Э°, как, например, в (2.22).

Свойства симметрии могут быть успешно использованы для анализа и синтеза 4Р-цепей. Пусть восьмиполюсник (рис. 2.3) симметричен относительно горизонтальной оси и ко входу / подключен

источник единичной амплитуды. Для анализа таких цепей весьма удобен метод синфазно-противофазного возбуждения (он будет использован в последующих главах).

Сущность этого метода заключается в следующем: фактический источник заменяется эквивалентной группой из 4-х источников, имеющих половинную амплитуду: двух (/, 2) синфазных на одном входе и двух (5, 4) противофазных, дающих в сумме нуль, на другом входе (как показано на рис. 2.3). Используя принцип суперпозиции, находим сначала результат воздействия синфазных источников / и 5 на разных входах, а затем- противофазных 2, 4. В первом случае по оси а - а взаимно компенсируются токи обоих источников, во втором - их напряжения. Таким образом вся 4Р-цепь делится на две более простые идентичные 2Р-цепи (четырехполюсники): Л+ - для синфазных и Л - для противофазных источников (рис. 2.4). Анализируя их в отдельности и затем суммируя решения, получаем результат воздействия одного фактического источника. Данную операцию можно записать в форме

(2.27)

Применительно к матрицам [5]+ и [S] для 2Р-цепей Л+ и Л справедливы следующие теоремы [14]. Теорема 2.1.

Если матрицы [5]+ и [5] для 2Р-цепей А+ и А~ различаются только знаками элементов главной диагонали, торезультирующая 4Р-цепь согласована на всехчетырех попарно-развязанных входах (обратное положение не справедливо).

Доказательство: пусть Sti = - Sfi = 7, а Sjb = = 5i2 = p. Тогда в соответствии с (2.27) вектор отражения, одинаковый на входах 1 н 4, составит

JLrn JLr Ц = \

2 [IJ 2 [-ij

Т. е. для исходной восьмиполюсной цепи = 544 = О, а 54 = = у. Передача ковходам 3 н 2 определится аналогичным образом:

т. е. входы / и 2 развязаны, а 5i3 =р. Подключив источник кТлюбомуиз входов 2 или 3, тем же путем] находим, что входы 2 Jii 3 согласованы, а входы Зп 4 развязаны. Теорема 2.2.

Если некоторые 2Р-цепи А+ uA-, нормированные к сопротивлениям нагрузок одной из пары входов, дуальны, то соответствующие матрицы IS]+

2 Зак. 10Г9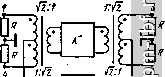

Рис. 2.4. Функциональная схема квадратурного устройства с дифференциальными трансформаторами и выделенными четырехполюсниками А+ и А-.