температурные допуски 0(АЛ 4), допуски на влажность D, (ДЛ/Л), изиоо D(AAIA), производственные допуски D{hA/A). Аналогично погрешностям допуски включают регулярную (средину поля допусков) и случайную (половину поля допусков) компоненту

D (ДЛ /Л) = М. (ДЛ/Л) * 6 (ДЛ/Л).

Суммарный эксплуатационный допуск устройства получают раздельным суммированием по регулярным н случайным компонентам всех типов допусков. В предположении взаимонезависимости перечисленных отклонений

D (ДЛ/Л) = е.[А1 р (ДЛ/Л) + (АЛ/Л) + Al (ДЛ/Л) + УИ (ДЛ/Л) +

+ ]/б^р,(АЛ/Л) + б? (ДЛ/Л) + L (ДЛ/Л) + 63 (ДЛ/Л), (15.26)

где 8 - коэффициент запаса на отклонение параметров под воздействием дестабилизирующих факторов, не учтенных при расчете, таких как механические воздействия, пыль, радиация, атмосферное давление и др. На основании [113] принимают в = 1,10 ... 1,20.

Исходя из вышеприведенного, может быть уточнено определение на-дежиостн по постепенным отказам, как вероятность того, что на заданном интервале времени t в заданных условиях эксплуатации действительное значение выходного параметра останется в пределах поля допусков

р„(0 = Р[ ДЛ/Л !< ID (ДЛ/Л) 1]. (15.27)

Вероятность Рд (О называют гарантированной надежностью.

Уравнение погрешностей системы

Рассмотрим задачу определения погрешности (отклонения) выходного параметра системы через заданные отклонения параметров ее элементов. Пусть выходной параметр системы определяется рядом параметров комплектующих элементов (15.25), откуда с учетом сделанных определений

Л4+ ДЛ = ф (ою Нг Дог. . . й + Да(, . апа+ Доп)-Допустим, что отклонения параметров от номинальных значений достаточно малы

ДЛ/Лв 1, Да а:в 1.

вследствие чего при представлении приращения выходного параметра рядом Тэйлора можно ограннчитьси членами первого порядка малости

п

дл/л = ( - ..... )д ,.

Осуществив переход к относительным приращениям, что позволяет складывать отклонения различных размерностей, можно получить уравнение погрешностей системы

п

ДЛ/Л = У an) Oi /Да\

дЩ Ф ( 1, .... а,-.....a )\ajt

Обозначим коэффициент влияния t-ro элемента . dffjai.....а;, ... , а„)

Ф(%.....а,..... ) 05.28)

АА/А

(15.29)

Полученные уравнения (15.28), (15.29) являются исходными для расчета эксплуатационных допусков всех перечисленных типов. Как видно из формулы (15.29), коэффициент влияния fe,. определяет степень влияния погрешности параметра t-ro элемента на погрешность выходного параметра изделия. Для его расчета необходим алгоритм работы устройства (15.25). Экспериментальное определение коэффициентов влияния производят по формуле

ki - ((ДЛ/Л)/(Да/а),-]д о

Да,- = Да,

Да< Да,-.

Да , полученной из уравнения погреш-

ностей (15.29). При этом задают достаточно малое приращение i-ro параметра при номинальном значении всех остальных и фиксируют соответствующее ему изменение выходного параметра.

Способы повышения надежности по постепенным отказам

Как видно нз выражений (15.27), (15.29), повышение надежности по постепенным отказам сводится к уменьшению отклонений выходного параметра системы АА/А, что может быть достигнуто двумя способами. Первый из них не отличается от способа повышения надежности по внезапным эксплуатационным отказам и заключается в улучшении качества элементов, т. е. в уменьшении отклонени!! параметров,элементов (Да/а). Второй предполагает уменьшение коэффициентов влияния k, т. е. улучшение качества отработки схемы на некритичность - свойства устройства сохранять значение выходного параметра в заданных пределах при существенном изменении параметров комплектующих элементов.

Экспериментальная отработка некритичности схемы (граничные испытания) заключается в выборе оптимальных значений параметров элементов схемы с позиций ее некритичности. Для проведения граничных испытаний выбирают выходной (определяющий) параметр схемы, например, для генератора - стабильность частоты или амплитуды, для триггера - переход из одного положения устойчивого равновесия в другое при нормированном воздействии. Далее снимают диаграммы граничных испытаний (рис. 15.9), которые определяют область устойчивой работы (показана штри-ховкой) в зависимости от изменения испытываемого параметра щ под воздействием /-го дестабилизирующего фактора (например напряжения питания, температуры, влаж-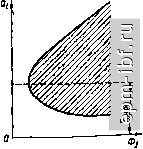

Рис. 15.9. Диаграмма граничных испытаний

ности, старения). Из диаграммы следует выбор оптимального значения a,-,-opt. который обеспечивает нормальное функционирование схемы в наиболее широком диапазоне изменений /-го дестабилизирующего фактора. Выбор оптимального значения J-ro параметра производят наложением диаграмм граничных испытаний по всем дестабилизирующим факторам Hi optijopv Описанный эксперимент может быть заменен моделированием на ЭВМ по алгоритму работы устройства (15.25).

Рассмотрим ряд схемных решений, обеспечивающих некритичность. Прежде всего отметим, что многофункциональные схемы более критичны к изменению параметров, чем схемы однофункциональные, поскольку параметры элементов в таких схемах выбирают не оптимально, а компромиссно, исходя из различных, а зачастую и противоречивых требований, которые необходимы для выполнения отдельных функций.

Существенные результаты дает применение схем с авторегулированием и применением отрицательных обратных связей, таких как схемы АРУ, АПЧ, авторегулирование выходной мощности, которые рассмот-рены в гл. 11. Во многих из них выигрыш в стабильности обеспечивается за счет того, что устойчивость схемы определяется пассивными линейными цепями, значительно более устойчивыми к воздействию дестабилизирующих факторов по сравнению с активными нелинейными элементами (транзисторами, диодами, интегральными схемами). В качестве примера рассмотрим стабилизацию коэффициента передачи усилителя с отрицательной обратной связью

Ко.с = К/(+К), (15.30)

где К - коэффициент передачи усилителя без обратной связи; р - глубина обратной связи. Преобразовав выражение (15.30), получим

/Со.е=1/(1/С + Р)>

откуда видно, что при условии 1 С < Р величина коэффициента передачи задается величиной Р, которая определяется отношением параметров пассивных элементов (например, резисторов) и может быть сделана достаточно стабильной.

Некритичность может обеспечиваться за счет введения ограничения параметров - например, схемы ограничения амплитуды при помощи ограничительных диодов, базового детектирования, изменяющегося эквивалентного затухания контура (гл. 9).

Некритичность может обеспечиваться также за счет специальных устойчивых методов обработки информации, например, модуляционная схема взамен усилителя постоянного тока, подверженного дрейфу нуля. Важно отметить, что дискретные устройства с двоичным кодом значительно устойчивее аналоговых средств обработки информации к воздействию постепенных отказов. Объясняется это тем, что дискретные устройства с двоичным кодом имеют только два устойчивых состояния, которые легче стабилизировать относительно внешних воздействий, чем аналоговую аппаратуру, где необходимо обеспечить устойчивость заданной характеристики.

В заключение рассмотрим вопрос об общем подходе к проектированию надежных радиоэлектронных устройств, как с учетом внезапных, так и постепенных отказов. Поскольку постепенные и внезапные эксплуатационные