Определение связи контура с А и нагрузочной цепями, исходя из требований селективности и ослабления на краях полосы пропускания, сводится к определению связей, необходимых для получения эквивалентной добротности Qg, которая удовлетворяет двойному неравенству (4.22).

Коэффициент связи с А при Яд = const

сво = *св opt y(QJQ,)-L (4.29)

Рассмотрим соображения по выбору связи с нагрузкой. Прн малом шунтировании контура следует принимать гад = 1. При этом = Q,

cba = cbopt]/(Q/Qs)-l-

В схемах, где имеют место низкие входные сопротивления зиачи-тельиые величины С„ и существенная нестабильность АС , Д/? полагают < ! Коэффициент трансформации можно найти из (4.28):

о = ]/ [(Q/Q )-il(4.30) Отношение Q/Q = Лду^/Лду находят, задаваясь допустимым ухудшением добротности колебательного контура в результате нагрузки на сопротивление /?д (обычно принимают Q/Q - 1, 2...2).

Возможен и другой подход, при котором накладывают дополнительное условие (4.25), обеспечивающее наибольший коэффициент передачи ВУ при заданной селективности и полосе пропускания:

о = У [(Q/2Q,)-l]/? ?o. (4.31)

Такой подход может быть реализован при условии выполнения неравенства Q/ 2Сэ> 1.

При приближенном расчете задают ухудшение селективности в результате влияния антенной цепи не более 25

Q /q3=l,25, (4.32)

откуда k = 0,5ft pt-

Для KB антенн вещательных радиоприемников со средними значениями параметров

св а < 0.5 Kwlo V Q. - o,3/>/q;.

Поскольку параметры ненастроенной А заранее не известны, ее связь с контуром k/ должна быть выбрана так, чтобы разброс этих параметров относительно номинальных не приводил к расстройке колебательного контура более допустимой. Для эквивалентной схемы рис. 4.8, а возможные разбросы А Сд = Сд jjijj, . .. Сд приводят к уходу собственной частоты кон-

тура Д^ка о -О.бДк^к, где

Д^к = вн max - вн. ср = - (вн max - вн mln): (4.33)

(bZ.3 = -м'МV( Z.3 - 1 /шСд). (4.34)

Следовательно,

свД <2 V(5max D (mir,- D (Д/ка о) (Сах Cin) - (4-35)

где

max = firax YсвA max min = га!!. V сва min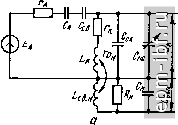

Сей

Рнс. 4.10, Эквивалентг!ые схемы входного устройства с внешнеемкостной связью с антенной

Ск.з

д

Гк.Н

Исходя из того чтобы при любой расстройке принимаемый сигнал оставался в полосе пропускания входного контура, обычно принимают Д/д < < 0,5Яду, откуда

Д/ка о < I/2Q3. (4.36)

Для KB антенн со средними значениями k 0,8/lQ .

Произведенные расчеты дают значения k < 0,2; обычно выбор feg является определяющим.

Схема одноконтурного ВУ с внешнеемкостной связью с А (рис. 4.3, в) может быть проанализирована как частный случай эквивалентной схемы рис. 4.8, а при Отсутствии трансформаторной связи (рис. 4.10, а). Коэффициент передачи ВУ находят из общего выражения (4.7) путем предельного перехода СБ -> ~ (I ->. оо), = 0:

/Сву = С,зП /? . jVl-i-x\

(4.37)

откуда резонансный коэффициент передачи

вуО = <ОоСсв 0о, э = о^кСсвЭэПиО-

При емкостной настройке контура изменения резонансного коэффициента передачи весьма значительно

ВУО max/ВУО min - 0 max/O min

При настройке о помощью вариометра = Qg/WoC.

КвУО = эиПоСсв/Ск = const, ективиости при произвольной

Ову = (fo/f) (л„о/л„) VTT

Выражение для селективности при произвольной расстройке может быть получено из (4.11):

(4.38)

где отношение no/n - (4.14, 4.15).

При определении ослабления по зеркальному каналу можно воспользоваться приближением

- ВУ як -

/fo max + 2f:

О max

0, Ьшах+2/

(4.39) 81

Ослабление на краях полосы пропускания определяется (4.21).

Для получения выражения рассмотрим эквивалентную схему рис, 4.10, б, в которой сделан переход к генератору тока /д = /шСд£д, а нагрузочная цепь /? Сд пересчитана в контур

Гк. н = + (У„к/Rn)

Произведем ряд последовательных преобразований, показаний на рис. 4.10, в, г, д, в результате чего, пренебрегая высоким внутренним сопротивлением генератора тока, приходим к схеме одиночного эквивалентного колебательного контура

Га в„ = (Са вн + } Ra] = [Сд в„/(Са в„ + к. (4.40)

q3 = Q/{1 + {nlRjR } + (Сд з„/(Сд з„ + С^. )]д/г,; (4.41)

к. э = к. н + А вн = к + н'н + А вп-

Для ненастроенных А часто принимают С^ < Сд, при этом Сд С^. Выбор емкости связи неоднозначен. Исходя из условия согласования, емкость связи контура с А

св opt == к. н \Ja емкость связи, допустимая по заданной селективности и ослаблению на краях полосы пропускания

св а ~~ к. н min

1/ l

емкость связи, допустимая по расстройке входного контура цепью А,

Ссвл<2

При малых разбросах Сд) ... Сд,, правая часть неравенства может неограниченно возрастать - это значит, что по соображениям расстройки контура А может быть включена непосредственно.

Из двух рассчитанных значений емкости связи С^ и С^ следует принять меньшее.

Соображения по выбору степени связи контура с нагрузкой (п^) не отличаются от изложенных выше (4.30, 4.31).

Схемы ВУ сдвухконтурным полосовым фильтром (рис. 4.5). Резонансный коэффициент передачи

ВУ0=/*ВУ1/0

где Kyi -резонансный коэффициент передачи одноконтурного ВУс той же степенью связи с Л и нагрузкой, что и рассматриваемый полосовой фильтр; т) = свэ ~~ параметр связи,

fecB- св М + св с = 1УЦ2 + / о к V2 . Qs = KOliOTz 91 = Ql/(1 + *св a/kIa); Оэг = q2/(l + >02/n).

где Qi, q2, Rdi - параметры ненагруженного первого и второго контура соответственно.