x(nTj х(пТ) д(пГ) у(пТ)

Дискретизатор

нис. Ъ.2Ъ С^1руктурная схема цифрового фильтра

формирования АЧХ, возможность оперативной перестройки фильтра в ходе обработки, высокая временная, климатическая стабильность параметров, отсутствие реактивных элементов, возможность реализации линейной ФЧХ. Могут быть достигнуты высокие значения добротности, точности. Отсутствует явление дрейфа, присущее аналоговым фильтрам. Возрастают возможности использования интегральной технологии.

К недостаткам ЦФ относят появление шумов квантования; необходимость преселекции; меньшее, чем в аналоговых фильтрах, быстродействие; сравнительно сложные схемные решения.

Классифицируют ЦФ по наличию или отсутствию обратной связи (рекурсивные, нерекурсивные); по порядку используемых звеньев (1-го, 2-го порядка и выше); по способу соединения звеньев (последовательные, параллельные); по частотным свойствам (ФНЧ, ФВЧ, полосовые, ре-жекторные).

Теория ЦФ базируется на линейных разностных уравнениях с постоянными коэффициентами (Z-преобразование, дискретная свертка). Используют также алгоритм БПФ.

ЦФ реализуются по такой же структурной схеме, как и другие устройства цифровой обработки информации (рис. 5.25). Ниже рассматриваются только собственно ЦФ (процессоры), а такие узлы, как дискретизатор, АЦП, ЦАП ч сглаживающий фильтр не затрагиваются, так как они не отличаются в ЦФ какими-либо особенностями.

5.3. Краткие теоретические сведения

Усилители с одиночными LC-контурами, настроенными на одну частоту

Основные расчетные соотношения для усилителей с одиночным настроенным LC-контуром (рис. 5.1...5.6, рис. 5.12) могут быть получены с помощью анализа обобщенной эквивалентной схемы рис. 5.26, а, где АЭ1 и АЭ2 представлены упрощенной эквивалентной схемой в системе К-параметров: Kji ~

проводимость прямого действия, 522= 1/-22 + /ШС22; 511= I/.R11-Ь

+ /шСц; К„= l/i? + /cDC ; г^, С^, Q = cd L/r, i? = QcD i - соб-

ственные параметры ненагруженного контура. При однотипных АЭ1 и АЭ2 К„= Кц. Пересчитав параметры АЭ1, АЭ2 параллельно контуру, получим эквивалентную схему рис. 5.26, б

22 ви= 22/ !. н. ви= -н/г;

22 ви = 22 !. и. вн = и^г!

откуда переходим к схеме с одиночным эквивалентным нагруженным контуром (рис. 5.26, в), где эквивалентная емкость

-к. 9 = + 22 ви + н. ви = + 122 + Щрп,

Аэг

о

n, n,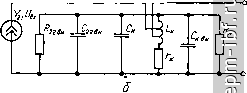

Рис. 5.26. Эквивалентные схемы усилителя с одиночным LC-контуром

эквивалентные сопротивление потерь, добротность и резонансное сопротивление

к. э = к + 22 вн + н. dh = к+ (nWtiLJR.,.,) + (niwlLJR) =

= о^к^-к. . = <?/tl + \RJR- + <Ro/R \, (5.17)

o. э = <?э 0/-к = RJl + i/?o/22 + -iRo/Rl (5- 18)

Эквивалентное сопротивление контура на произвольной частоте

i о. э I = о. jV-

где обобщенная расстройка х - Q[{f /fg) - (/ )], для случая малых расстроек x = Q2iS.I/fg. Как следует из рис. 5.26, в.

(5.19)

вмх=5211/вХ ЛЛо.з/У 1+Л

откуда коэффициент усиления

К = вых/вх = 1 2 I У,! i -о. э/У^Т^

коэффициент усиления на резонансной частоте

Kg = п,п^ I I э = I Уп 1 Ло/ I 1 + ( l/?o ?22) + ( 2o/h)]- (5-20)

Из формул (5.19), (5.20) можно найти селективность каскада

а = Кд/К = (1 Ki !о/1 У \) VTT. селективность при малых расстройках

о = Vr+ЩШо).

неравномерность АЧХ на границах полосы пропускания

(5.21) (5.22)

выражение ФЧХ 120

n = Vl + iQ,n/fg)\

ф = arctg x.

(5.23)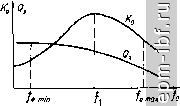

Рнс. 5.27. Зависимости резонансного коэффициента усиления н эквивалентной добротности от частоты

Зависимость резонансного коэффициента усиления и эквивалентной добротности от частоты настройки усилителя показана на рис. 5.27. На малых частотах (/ <: fi), где изменение параметров АЭ (F21, /?22. ~ Rn) сравнительно невелико, Q изменяется незначительно и рост Ко определяется ростом волнового сопротивления ЩЕ, На более высоких частотах (/>/1) перечисленные параметры АЭ уменьшаются,

увеличивается шунтирование контура, что приводит к снижению усилительных и селективных свойств усилителя.

Для /У-каскадного усилителя справедливы следующие соотношения для коэффициента усиления, селективности н коэффициента прямоугольности;

KiKg/VT+lf, =( 1 .1 Y \YT+7)\

= Я,/Я = К(усг^-1)/(/2-1). где Па к П - полосы пропускания при заданном ослаблении а и на уровне V2. Значения kaW nioo> пЮоо приведены в табл. 2.7.

Оптимизация каскада по мощности позволяет передать максимальную мощность сигнала от АЭ1 к АЭ2 при заданной неравномерности АЧХ в пределах полосы пропускаиня П. К такой оптимизации прибегают в тех случаях, когда поглощение мощности нагрузкой становится существенным, например, при использовании биполярных транзисторов или ИС. Область применения - широкополосные каскады УПЧ с разделением функций селективности и усиления, УСЧ с непредъявленнымн требованиями по селективности и относительно высокими требованиями по усилению (СВЧ приемники). Рассмотрим условия согласования (рнс. 5.26)

G + niG22 = n2optGH. (5-24)

где проводимости Gq = l/Rg-, G-i = UR22; G = 1 ?, откуда

2opt = VGg/G + nlG /Gg = V RJRg + niRJR,. (5.25)

Подставив (5.25) в (5.20) н (5.17), получим выражения оптимальных значений коэффициента усиления н эквивалентной добротности

0 opt = i i VrJ VRJnlRg+\; (5.26)

<33opt = <3/2( i4/22+l). (5.27)

Как видно нз (5.26), для увеличения Ка, и упрощения конструкции целесообразно принять 1 = 1, если это допустимо по соображениям устойчивости, стабильности параметров контура и перекрытию частотного диапазона. Прн этом после ряда преобразований

0 opt = I 2110/2 KG (G + G22),

Q3 pt = Q/2[/? ?22 + U-6 7-230 1 21