При условии Go С G22. что характерно для биполярных транзисторов,

Oopt = l>2.o/2KG G2,.

(5.30)

Формула (5.30) удобна при расчете структурных схем. Исходя из выражения (5.27), можно рассчитать эквивалентную емкость контура

3 = 0/а)о/? = [I/2Q3 - 1/Q],

(5.31)

где Q = fjn, откуда параметры контура

Ск = Ск.э-( :С2.-П2орЛ). (5.32)

/. = 2,53. Ю'/С^.з, (5.33)

где / - кГц; С -пФ; L -мкГн. С учетом емкости схемы С^, = С^, + C контурный конденсатор Cq~C - C. Полученный результат (5.33) следует сравнить с минимально реализуемой индуктивностью контура l., которая в зависимости от частоты / приведена в табл. 5.1. Если -к<кт1П' следует принять

Ск. 3 = 2,53 . lO-o/ZoL.

(5.34)

Таблица 5.1. Минимальные индуктивности контурных катушек

В случае G G22 О, rtj = 2 = 1 (АЭ с высокоомным входом и выходом, в частном случае каскад на полевом транзисторе) контурную емкость определяют из следующих соображений. С одной стороны следует уменьшать С^, поскольку при этом усилительные свойства каскада улучшаются

Ко = \Уп ! /? = S/? = SQ/w C3.

С другой стороны, эквивалентная емкость контура должна быть настолько большой, чтобы расстройка конгура за счет разброса АС нестабильных емкостей С^, С22, G не превышала допустимую

С^.з>(1,5...2) ДС(/ /Я).

Кроме того, должна быть обеспечена необходимая устойчивость, что рассмотрено ниже.

Обеспечение эквивалентной добротности кон'гура здесь достигается либо выбором контурной катушки с соответствующей добротностью, либо шунтированием контура дополнительным резистором

Сш= = со С^.з(1/Оз-1/(?).

Расчет с позиций заданных селективности и неравномерности АЧХ в пределах полосы пропускания проводят в узкополосных УСЧ и реже в УПЧ

<5-О-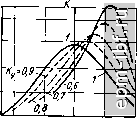

-55 О 0,5йЩ5П 6

Рнс. 5.28. Эквивалентная схема н АЧХ усилителя с одиночным 1.С-контуром

С распределенной селекцией приемников низких групп сложности. Первоначально из двойного неравенства

(5.35)

определяют эквивалентную добротность Q3, где частные эквивалентные добротности, необходимые для обеспечения заданных значений o = a3j3,

этз. к = Ко2 тз - /(/з. к о - /о з. к);

(5.36) (5.37)

Эквивалентную добротность (5.35) при заданных параметрах ненагруженного контура (Q, /?о) и параметрах нагрузки (/?22. реализуют путем подбора коэффициентов согласования rtj, 2 по формуле (5.17)

% = 0/(1 + >о ?22 + ,/?о ?н)-Рассмотрим два частных решения, которые обеспечивают дополнительное качество. Наложив ограничение (5.24), которое обеспечивает оптимизацию по мощности, сведем (5.17) к (5.27), откуда = njopj,

1 =/(/?22/Ло) (Q/2Q3-I). (5.38)

Как видно из (5.38), условие реализации этого решения Q/2Q3 > 1. Второе частное решение rti = 1 обеспечивает упрощение конструкции контурной катушки индуктивности. При этом из выражения (5.17) следует

2 = К(? ?о) (Q/Q3-?o ?.2-l)- (5.39)

Как видно из выражения (5.39), условие реализации этого решения

Q/Qs > 1 + /?о ?22-

Устойчивость каскада характеризуется степенью изменения усиления, полосы пропускания, формы АЧХ (ФЧХ) и других показателей; определяется внутренней обратной связью АЭ через проводимость обратного действия Fja (рис. 5.28, а). Рассмотрим представленную здесь эквивалентную схему каскада, где АЭ характеризуется матрицей К-параметров

УЧ,\ 2

[К] =

источник (генератор) и нагрузка со входа и выхода АЭ

0 =Со/п2.

Как известно, входная проводимость четырехполюсника может быть представлена в виде

22 Г

где AJbx ~ приращение входной проводимости АЭ, обусловленное действием обратной связи. Активная составляющая этой проводимости

где

Gil = Re (Уи), ДОвх = Ке[-УЛ/(522 + 5н)]- (5.41) Запишем коэффициент устойчивости в виде

= (G, + Gn + AG3 3,)/(G, + Gn). (5.42)

характеризующем устойчивость усилителя в широком смысле [122], т. е. определяющем, как степень удаленности от самовозбуждения, так и степень искажения АЧХ (ФЧХ) под действием обратной связи, где AG = ~ fBx ()]max- видно из (5.42) О < < 1, при отсутствии обратной связи &у= 1, при самовозбуждении йу = 0. Исследование на экстремум выражения (5.41) показывает

AG.a, = i I 1 1/2 (G., + G ). (5.43)

Подстановка (5.43) в (5.42) позволяет получить выражение

y=i~[\Yi;\\y-n\/2GuG {\ +Ai)il+A,)], (5.44)

где показатели связи входной и выходной цепи АЭ с генератором и нагрузкой А, = Gp/0 , A., = GJG.

Приравнивая А^ = А^ - А по условию достижения максимального усиления, получим

*у = 1 -1! 5i2 М zi I /2G G22 (1 + АП (5.45)

откуда обобщенный показатель связи

А = G,/Gi, =3 GJG (5.46)

может быть выражен через параметры АЭ и заданную устойчивость

= V\Yi,\\y \/[2GiiG (\-k)] I. (5.47)

Исходя из (5.40), (5.46), (5.47) по заданной устойчивости, параметрам АЭ и ненагруженного контура можно рассчитать необходимые коэффициенты- трансформации

п, = KG /AG , = /G /AG,i- (5.48)