Рекомендуемые значения коэффициента устойчивости

<0,92 высокая устойчивость,

=0,8...0,92 - средняя устойчивость, f5.49)

=0,7...0,8 - низкая устойчивость.

На рис. 5.28, б в качестве примера показаны АЧХ одноконтурного усилителя К {А[/05П) для ф= arg [К12К21] = 90° для различных значений В заключение приведем выражение для устойчивого коэффициента усиления каскада по напряжению

2(1-fey) (5.50)

Усилители с одиночными попарно-расстроенными LC-контурами

Область применения - широкополосные и узкополосные УПЧ. Коэффициент усиления двухкаскадного УПЧ (рис. 5.15, а) в предположении Ro.s/ о.э2 - о.э вычисляют по формуле

У (I+xl - xY + ix К (1+ 2 -л;2)2 + 4л;2

где /Со1 - резонансный коэффициент усиления резонансного каскада; д: - обобщенная расстройка контуров относительно средней частоты (5.7). Вследствие отмеченной выше бимодальности К (ш) пользуются двумя видами АЧХ: селективные свойства оценивают по характеристике у = 1/а = К/Ко< неравномерность по характеристике 7= \/а^[ = KlK,- При малых расстройках х„ < 1 АЧХ одногорбая с максимумом, расположенным на частоте / ,

/С„ = /С„ах = /Со1/(1+ ) (5.52)

(/ = V = (1 + р/ V(\ +xl-xY + Ax (5.53)

При критической расстройке *о ~ ЧХ уплощается

Ко = /тах = 01/2; (5.54)

(/ = V=2 :?T4. (5.55)

При увеличении расстройки о > АЧХ становится двугорбой с провалом иа частоте/о и с максимумами при расстройках

При подстановке х - х^. в формулу (5.51) получим

шах = </2А^.; (5.56)

y=(x + xl)lV(\+xl- х^) + Ах; (5.57)

y = 2xolV{\+х1-х^)+Ах\ (5.58)

Из формулы (5.58) следует выражение для глубины провала на центральной частоте (рис. 5.15).

V = 2V(1 + *о). -(5-59)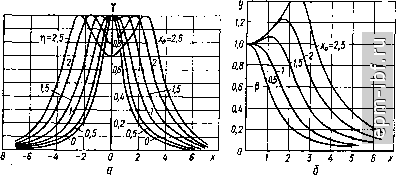

Рис. 5.29. АЧХ УПЧ с одиночными попарно-расстроенными контурами или с двухконтурным полосовым фильтром

Рнс. 5.30. Зависимости глубины провала АЧХ УПЧ с одиночными попарно-расстроенными контурами (илн ДПФ) от обобщенной расстройки (или фактора связи) н числа каскадов

откуда МОЖНО рассчитать величину предельной расстройки, необходимой для обеспечения заданной неравномерности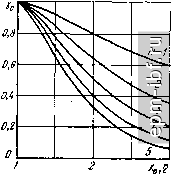

= а„+Уа-1. (5.60)

При переходе к Л^-каскадному усилителю выражения (5.52)...(5.59) следует возвести в степень n12.

На рис. 5.29 приведены характеристики V (х), у (х), построенные для двухкаскадиого УПЧ при различных значениях по формулам (5.53), (5.55), (5.57), (5.58). Зависимости Y [х^, N) (5.59) показаны на рнс. 5.30. Значения коэффициентов прямоугольности ц шо различного числа

каскадов при критической и предельной расстройках приведены в табл. 2.7.

Трехкаскадный усилитель с одиночными LC-KOHTypaMvi, настроенными на три частоты

Коэффициент усиления

К = К^Кдз/ УЮ +-xl-xY + 4x]0+xl). где Коз и Хз - резонансный коэффициент усиления и обобщенная расстройка каскада, настроенного на среднюю частоту /о.

При хо < 1,75 суммарная АЧХ одногорбая, а при > 1,75 - трех-горбая. Ординаты всех максимумов равны при условии

Оз1 = е,5(3,2.

где и - соответственно эквивалентные добротности контуров, настроенных на частоты fo ± AF. При этом уравнение АЧХ

= 2 (1 + xl)/V[(\ +х1-ху + 4х^]{4 + х%

Усилители с двухконтурными полосовыми фильтрами

Эквивалентная схема усилителя с двухконтурным настроенным иа среднюю частоту полосовым фильтром (ДПФ) показана на рис. 5.31, где пересчет параметров АЭ в контур (Лзгвн- 22вн> н. вн- п. вн выполнен по формулам, приведенным для схемы рис. 5.20, б. Полагая контуры одинаковыми /,1 = / = /о, ri = = к. = к2 = к. = к2 = к, получают выражение коэфс{)ициента усиления каскада

вх V(\ + - х-У + Ах /(1 +Т)2 л:-)2 + 4л:2

(5.61)

где ;с = Оз (2Д/, ); = /(Зэ1<3э2; <3э1 = <3/( + ni/? /2.S; Оэ2 = Ql +

+ I/o/Rh) 1 = *св<Ээ; cb = /V. oi = i 2l 522 о.э- Сравнение формул (5.51) и (5.61) показывает, что их знаменатели, определяющие частотные свойства, полностью совпадают при условии замены обобщенной расстройки х^ на фактор связи г|- Это обстоятельство позволяет распространить выводы, полученные для усилителя с одиночными попарно-расстроенными контурами на усилитель с ДПФ. При малых связях г) < 1 АЧХ одногорбая с максимумом, расположенным на частоте /

(5.62)

г/ = Y = (1 + +ii2-x2)2 + 4;c2. (5.63)

При критической связи rip = 1 АЧХ уплощается - см. (5.55), Ко - - 4K.uil2. При увеличении связи более критической г\ > 1 АЧХ становится двугорбой с провалом на средней частоте /о и с максимумами при расстройках

.=ziz Fri - 1,

(/=(!.+ ri) (l + Л^-)+4л:;

Y = 2ri /(1 + - 2)2 4.2;

Ko = r\Koxl(\ + r\-);

70 = 211/(1 + 11);

(5.64) (5.65) (5.66) (5.67)

(5.68)

При переходе к Л'-каскадному усилителю выражения (5.62) ... (5.67) следует возвести в степень N.

На рис. 5.29 приведены АЧХ у (х), у (х), построенные для каскада ДПФ при различных значениях фактора связи по формулам (5.63), (5.55), (5.64\ (5.65). Зависимости Yq (г|, N), построенные по (5.67), показаны на рис. 5.30;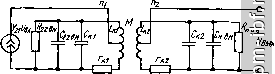

Рис. 5.31. эививалентная схема упч с двухкоитуриыми полосовыми фильтрами