При реализации ФСС необходима тщательная экранировка контуров. Поскольку форма АЧХ зависит от отклонений параметров элементов звеньев от расчетных, последние ие должны превышать 5 %.

ФСС с LC-фильтрами Чебышева и Баттерворса

Эквивалентная схема каскада с полиномиальным дг-коитурным фильтром Чебышева (Баттерворса) представлена иа рис. 5.20, а, где проводимость генератора = G, + /шС = G + / Саз, проводимость нагрузки = = Од -f- /шСд. Каждый из контуров с учетом элементов связи настроен иа срзднюю частоту полосы пропускания

С = С тэ т

/о = 1/2я /Тс7з = 1/2я УЩ = . . . = 1/2я УТС, = Ci + nlC + Ci C23 = С, + Ci + С,з

Is = 2э = = тэ = э. где коэффициент связи между контурами

12 = 12/3, ЙаЗ = Сзз/Сз, fem-l,m = m-l,m/9-

(5.84)

(5.85) (5.86)

(5.87)

Фильтры Чебышева дг-го порядка обладают следующими свойствами. В пределах полосы пропускания для 1 А<о , <: 1 значения нормированной передаточной функции 1 К (/Аш) = ! 1/а (х) \ колеблются в пределах 1/(1 W) п I. На интервале О <: Д<о I 1 имеется т экстремальных точек, в которых функция 1 К (/А<о) ! достигает максимального (минимального) значения - по этой причине фильтры Чебышева называют равиовол-новыми. В качестве примера на рис. 5.34, а приведены зависимости iC (/Асо) i, определяемые выражением (5.10), иа участке О < Аш <: 1 для числа контуров 2 ... 6. Второе свойство фильтров Чебышева состоит в том, что при i А<о| > 1 функция I К (/А<о) 1 монотонно убывает и стремится к

высоких

нулк . Крутизна спада (рис. 5.34, б, а„ = 3 дБ).

частотах составляет 20 дБ/декаду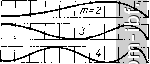

60 80 100 120

2 4 бЩрад/с

О 0,2 ДА 0,6 йш,рад/с

а б

Рис. 5,34, Амплитудно-частотные характеристики фильтров Чебышева

Как указано в п.5.2, для получения максимальной прямоугольности характеристики селективности (ХС) нужно, чтобы модуль селективности изменялся по закону (5.10)

где полином Чебышева дг-й степени от аргумента х

( cos (дг arccos х) при л;< 1;

Г„(д;)= (5.88)

1 ch (т arch л:) при л; > 1,

обобщенная расстройка х = [fjri) 2A /d; W - волновость ХС. Из приведенных выражений следуют основные характеристики ФСС: иеравиомериость ХС в пределах заданной полосы пропускания П, при заданной волновости (5.11)

необходимая волновость при заданной неравномерности ХС в пределах полосы пропускания П

й7 = ал-1, (5.89)

селективность по СК при заданном числе контуров и волновости для случая с.к )

c.K=V r (c.K). (5.90)

число контуров, необходимое для получения заданной селективности и неравномерности ХС в пределах полосы Я (волновости)

m> Ig(2а JVw)l\g{x + Vxl~\). (5.91)

Отправляясь от известной волновости W (5.89) и числа контуров т (5.91), можно произвести расчет полюсов передаточной функции

Pi = -sh I sin [(я/2т) (2i - 1)] +

--/chcos[(n/2m)(2i-1)] (5.92)

и необходимой добротности (5.12)

Q>/o/Яshgsiп(я/2ffг), (5.93)

где

e = (l/m)arsh(l W). (5.94)

Для фильтра Чебышева, как и для фильтра Баттерворса, передаточная функция К (р) имеет одни только полюсы; ее числитель представляет собой постоянную величину и не содержит нулей при конечных значениях частоты. Как следует из (5.92), полюсы фильтра Чебышева расположены на эллипсе в левой полуплоскости р. Для рассматриваемых фильтров при дг > 3 для получения оптимальных характеристик необходима различная добротность контуров, При этом целесообразно принять

Q2= Q3= ...= 1= Q <Qi. (5.95)

где

l/Qi = -(m-l)/Q-J Pf. (5,96)

0,8 0,6

ол о, г

О 1 2 А (J, рад/с

Рис. 5.35. Амплитудно-частотные характеристики фильтров Баттерворса

На базе известных полюсов pi, pi, р, и добротиостей Qi, Qi, может быть выполнен синтез схемных элементов: контурных конденсаторов Cj, С;, С„, иидуктивностей L и конденсаторов связи Cjj, Cj- , ( Графо-

аналитическая методика такого расчета приведена в [45, 47].

Фильтры Баттерворса т-то порядка обладают следующими свойствами. Функции модуля передачи имеют максимальное значение при Д<о == О и монотонно убывают при 1 Лй) 1 > 0. При этом частота среза по уровню 3 дБ равна 1 рад/с, крутизна спада АЧХ составляет 20 дБ на декаду (рис. 5,35).

Второе свойство состоит в том, что первые (2т - 1) производные АЧХ фильтров т-го порядка равны нулю при Дш = 0. По этой причине фильтры Баттерворса называют фильтрами с максимально плоской АЧХ,

Как указано в п, 5,2, ХС фильтра Баттерворса может быть представлена

в виде (5,13):

а(д;) =/l + Ух-г ,

где параметр V определяет неравномерность ХС на границе полосы пропускания. Из выражения (5,13) следуют основные характеристики ФСС: неравномерность ХС в пределах заданной полосы П (5.24) при заданном параметре V:

значение параметра V при заданной неравномерности ХС в пределах полосы пропускания П:

(5.97)

селективность поСК при заданном числе контуров и параметре К для случая

(5,98)

число контуров, необходимое для получения заданной селективности и неравномерности ХС в пределах полосы П (параметре V)

>lg[(o,k-l)/n/2!ge.k- (5.99)

Отправляясь от известного числа контуров т (5,99) и параметра V (5,97), можно произвести расчет полюсов передаточной функции

Р1 = к- [-sin (я/2т) (2( - 1) + / cos (я/2т) (2( - 1)] (5.100)