Рис. 5.42. Каноническая функциональная схема цифрового фильтра

->

* гч. w

Ha рис. 5.43 показана функциональная схема ЦФ, образованного параллельным соединением цифровых звеньев 1-го порядка, а на рис. 5.44 - последовательная функциональная схема, состоящая из звена 1-го порядка и звеньев 2-го порядка (звенья более высоких порядков практического применения не находят).

При проектировании ЦФ первоочередной целью является определение системной функции Я (Z). По известной Я (Z) легко определяются частотные (АЧХ и ФЧХ) и временные (импульсная и переходная) характеристики фильтра. Системная функция ЦФ - это отношение Z-преобразования выходного сигнала к Z-преобра-зованию входного сигнала

Рис. 5.43. Функциональная схема цифрового фильтра с параллельным соединением цифровых звеньев

Я (Z) = Z {{/ (nT)]lZ {X (пТ)].

5М

-021,

V(ri.

Рис. 5.44. Функциональная схема цифрового фильтра с последовательным соединением

цифровых звеньев

Эта функция аналогична коэффициенту передачи аналогового фильтра в операторном виде

К (Р) = у (Р)Ы (р).

Системная функция может быть получена из разностного уравнения ЦФ при замене переменных Z-преобразованием. Так, для нерекурсивного ЦФ

Я(2) = 2 CiZ-i

системная функция содержит только нули (С, - вещественный коэффи цнент).

Для рекурсивного ЦФ

L м

Я(7) = (5] 6,Z-)/(l+ S ftrnZ-). /=0 m=l

Одиим^из наиболее простых и распространенных методов проектирования ЦФ является метод билинейного преобразования. Выбирается исходный аналоговый фильтр, так что заданной является функция К (р). Далее производится замена переменной р на Z по формуле билинейного преобразования

р= (1 + (5.114)

Полученная после преобразований функция является системной функцией ЦФ.

Преобразование (5.114) сопоставляет р-плоскость и Z-плоскость. Для получения частотных характеристик нужно установить связь между координатами точек вдоль частотной оси р-плоскости - сод для аналогового фильтра и координатами точек, лежащих на единичной окружности Z-плоскости - сОц для ЦФ. Подставив в (5.114) р - jcoji и Z = е/мТ получим

соотношение, связывающее Шд и сОц,

Щд = tg (сОцГ/2),

где сОд = (й/Ид - безразмерная частота.

Рассмотрим методику расчета, ориентированную на применение ЭВМ, которая позволяет свести к минимуму объем подготовительных операций и наиболее целесообразна при расчете фильтров высоких порядков. Предположим, что синтезируемый ЦФ реализуется каскадным соединением рекурсивных блоков второго порядка, построенных по канонической форме (так называемых биквадратных блоков), структура которых представлена на рис. 5.45. Системная функция биквадратного блока имеет вид

Н (Z) = (а„ + OiZ-i + a,Z-)/(l - bZ- - b,Z-). (5.115)

Полосовой ЦФ реализуется последовательным включением фильтров нижних и верхних частот, причем порядок их соединения при реализации фильтра в виде npoi раммы для ЭВМ может быть произвольным.

Расчет производят в следующем порядке. По заданным требованиям к неравномерности АЧХ фильтра в полосе пропускания и полосе задерживания выбирают подходящий вид аппроксимации аналогового ФНЧ-прототипа. Далее определяют минимальный порядок фильтра и при необходимости до-

полняют его до ближайшего четного. При расчете полосового фильтра с неодинаковыми требованиями к крутизне скатов АЧХ со стороны нижних и верхних частот находят отдельно порядок ФНЧ и ФВЧ. По принятому виду аппроксимации и рассчитанному порядку фильтра находят значения полюсов системной функции, используя таблицы полю- сов из какого-либо справочника [68]. . Для каждой пары комплексно-сопряженных полюсов аналогового фнльт-ра-прототнпа вычисляют соответствующие координаты полюсов биквадратного блока 1 с помощью соотношений для билинейного преобразования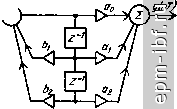

Рис. 5.45. Функциональная схему биквадратного блока

Z <= (1 + kp)l{\ - к^цР) - для ФНЧ;

(5.П6)

2п= (1 + Рк/квч)/{Рх/квч- I) - для ФВЧ,

где р^= о + /со - нормированный полюс прототипа; k = tg (л/р^ц д); к^ц = = tg (л;/(,зц д) - коэффициенты деформации частотного масштаба при билинейном преобразовании; /д ~ частоты среза АЧХ и дискретизации соответственно. Из (5.И6) определяют коэффициенты в обратных связях 6i = 2Re(Z ), 62 = -Z 2. .

В прямых связях принимают: для ФНЧ = 2; для ФВЧ Oi = -2; о ~ ~ независимо от вида фильтра.

Для расчета АЧХ одного блока используют выражение, получаемое из

(5.115) подстановкой Z= е'

Н (/u)) = (2cosu)/ +а^.)М1 + 26. (6.-1) cos (оГ-26. cos 2й)Г].

Суммарная АЧХ фильтра определяется как произведение АЧХ отдель-

ных блоков

где N - общее число блоков в фильтре.

Нормировка коэффициента передачи фильтра в полосе пропускания к единице производится включением перед фильтром нормирующего множителя

о„ = Я(/а)Г) i;.

Приведенная в гл. 3 программа F1LTR1 реализует один из методов синтеза нерекурсивных фильтров - метод взвешивания. Суть метода заключается в следующем. Известно, что импульсная характеристика фильтра связана о его частотной характеристикой преобразованием Фурье

Л (га) = 2 J Я (е' ) e du). -оо < л < оо.